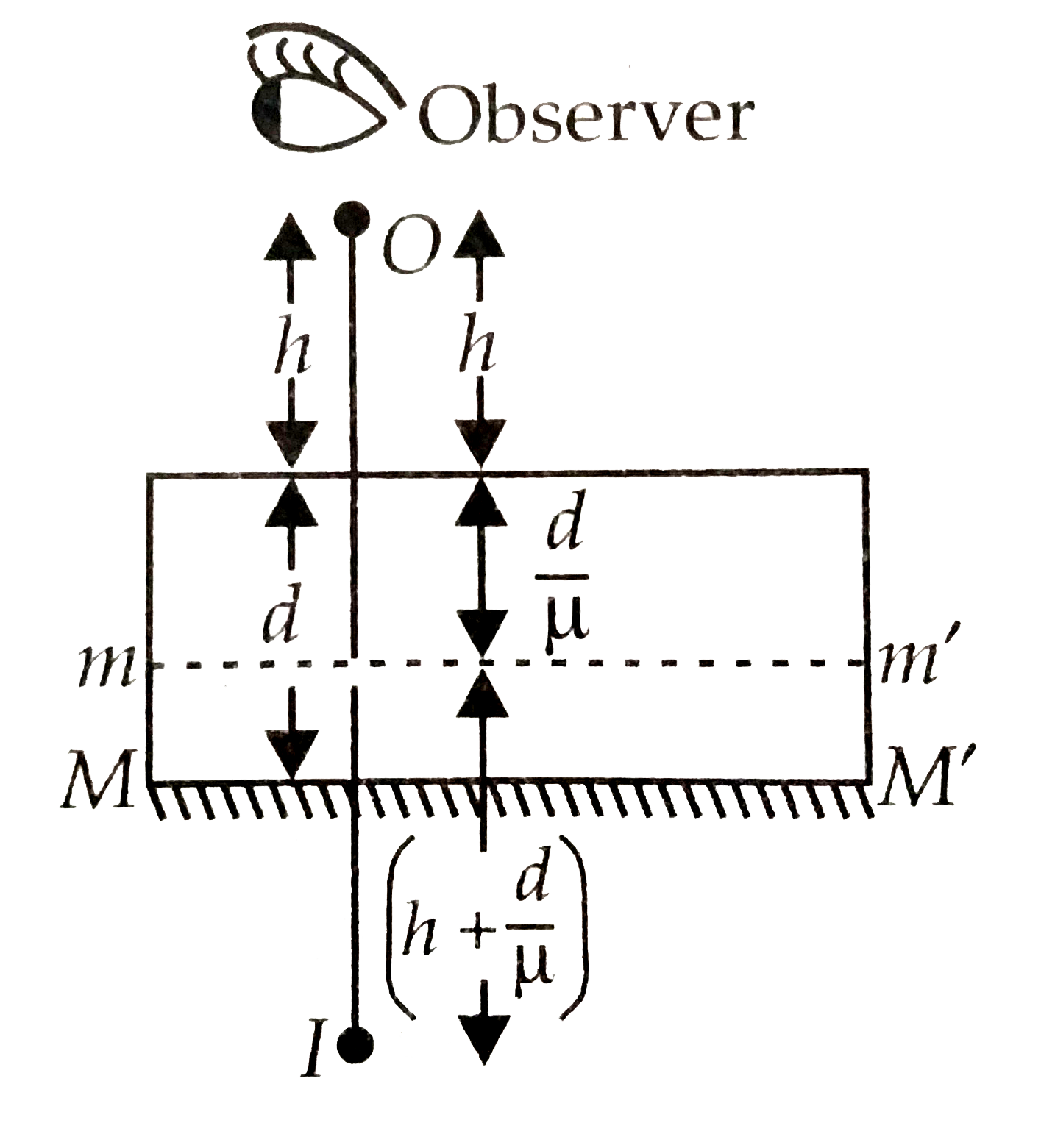
A point luminous object (O) is at a distance h from front face of a glass slab of width d and of refractive index μ. On the back face of slab is a refracting plane mirror. An observer sees the image of object in mirror as shown in figure. Distance of image from front face as seen by observer will be

h+2dμ
2h+2d
h+d
h+dμ
The correct Answer is:A
As shown in figure glass slab with form the image of bottom i.e., mirror MM' at depth (dμ) from its front face. So the distance of object O from virtual mirror mm' will be h+(dμ)
Now as a plane mirror forms image behind the mirror at the same distance as the object is in fornt of it, the distance of image I form mm' will be h+(du) and as the distance of vir tual mirror from the front face as seen by observer =[h+dμ]+dμ=h+2dμ
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTIPSCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Total Internal Reflection
7 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTIPSCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection At Spherical Surfaces And By Lenses
41 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTIPSCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assertion And Reason
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTIPSCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
An object is at a distance of 0.5m in front of a plane mirror. Distance between the object and image is
View SolutionA point object O is placed at a distance of 62 cm in front of a concave mirror of focal lengthf=20cm. A glass slab of refractive index μ=32 and thickness 6 cm is inserted between the object and the mirror. Let’s define final image as image formed after the light ray originating from O passes through the slab, gets reflected from the mirror and then again passes through the slab. At what distance d from the mirror, the face AB of the slab can be placed so that the final image is formed inside the slab itself?

View Solution
Knowledge Check
A point luminous object (O) is at a distance h from front face of a glass slab of width d and of refractive index μ. On the back face of slab is a reflecting plane mirror. An observer sees the image of object in mirror as shown in figure. Distance of image from front face as seen by observer will be
 Ah+2dμB2h+2dCh+dDh+dμ
Ah+2dμB2h+2dCh+dDh+dμAn object is at a distance of 0.5m in front of a plane mirror. Distance between the object and image is
A0.5mB1mC0.25mD1.5mA point object O is placed in front of a concave mirror of focal length 10cm. A glass slab of refractive index μ=3/2 and thickness 6cm is inserted between the object and mirror.

Q. Find the position and nature of the final image when the distance x shown in figure, is 5cm.A11cm, virtualB17cm, realC14cm, realD20cm, virtual
A point object O is placed in front of a concave mirror of focal length 10cm. A glass slab of refractive index μ=3/2 and thickness 6cm is inserted between the object and mirror.

Q. Find the position and nature of the final image when the distance x shown in figure, is 5cm.
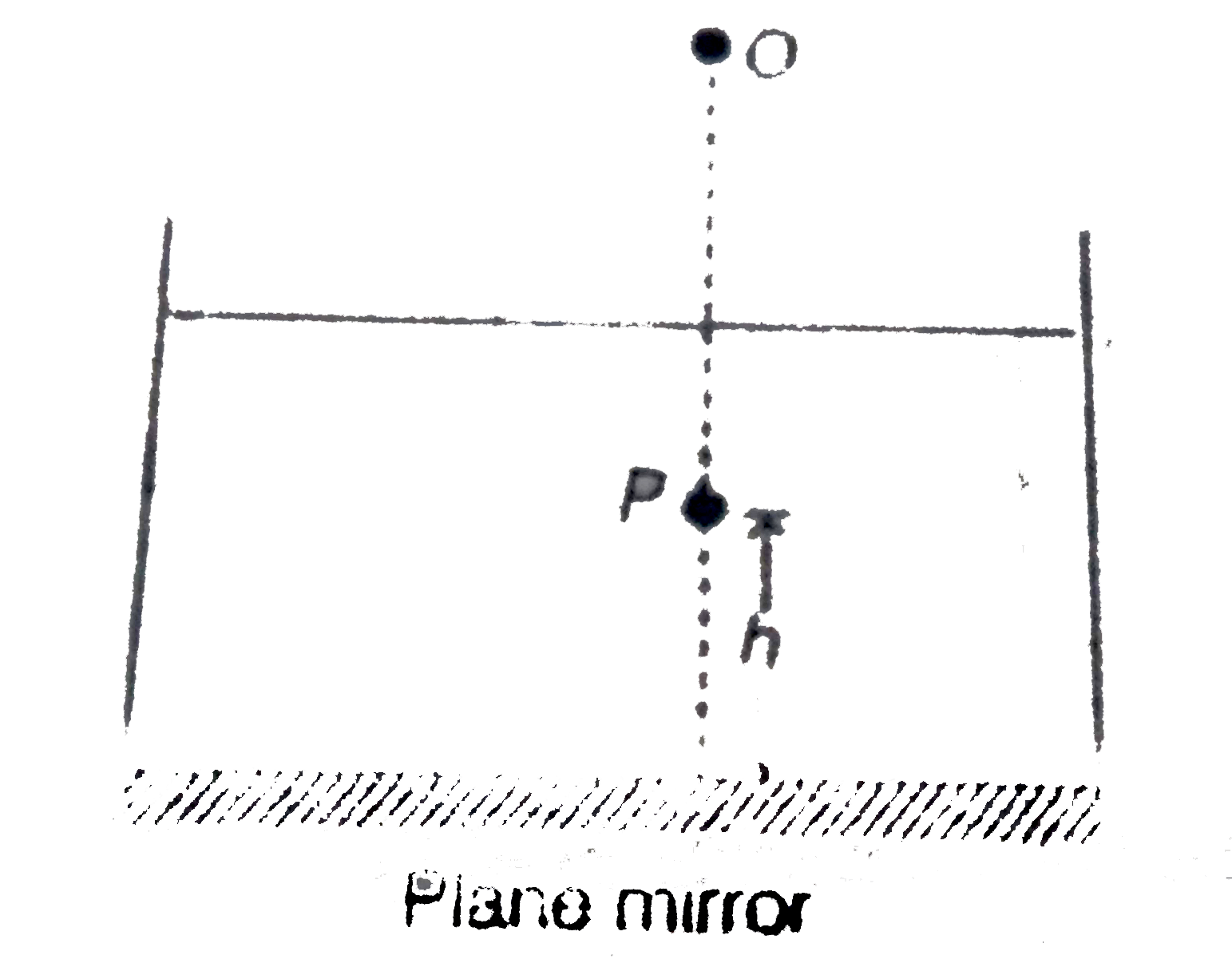
View SolutionA plane mirror is placed at the bottom of a tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observer observes P and its image in the mirror. The apparent distance between two will be
View SolutionFind the distance of object placed in the slab of refractive index μ from point P of the curved surface of radius R so that image is formed at infinity:

View SolutionA point object O is placed in front of a concave mirror of focal length 10cm. A glass slab of refractive index μ=3/2 and thickness 6cm is inserted between the object and mirror.

Q. Find the position and nature of the final image when the distnace x shown in figure, is 20cm.
View SolutionAn object is placed at a distance of 10 cm in front of a plane mirror, then the distance of image from mirror is:
View Solution
