The ratio of kinetic energy of a planet at perigee and apogee during its motion around the sun in eliptical orbit of ecentricity e is
`1:e`
`((1-e)/(1+e))^(2)`
The correct Answer is:C
To find the ratio of the kinetic energy of a planet at perigee and apogee during its motion around the sun in an elliptical orbit of eccentricity e, we can follow these steps:
Step 1: Define the distances at perigee and apogee
The distances from the sun to the planet at perigee (rp) and apogee (ra) can be expressed in terms of the semi-major axis a and the eccentricity e:
- At perigee:
rp=a(1−e)
- At apogee:
ra=a(1+e)
Step 2: Use the conservation of angular momentum
The angular momentum L of the planet is conserved. Therefore, we can write:
L=m⋅vp⋅rp=m⋅va⋅ra
where vp is the velocity at perigee and va is the velocity at apogee.
Step 3: Express the ratio of velocities
From the conservation of angular momentum, we can derive the ratio of the velocities:
vpva=rarp
Step 4: Substitute the expressions for rp and ra
Substituting the expressions for rp and ra:
vpva=a(1+e)a(1−e)=1+e1−e
Step 5: Find the ratio of kinetic energies
The kinetic energy KE is given by:
KE=12mv2
Thus, the ratio of the kinetic energies at perigee and apogee is:
KEpKEa=12mv2p12mv2a=v2pv2a
Substituting the velocity ratio:
KEpKEa=(vpva)2=(1+e1−e)2
Final Result
Thus, the ratio of the kinetic energy of the planet at perigee to that at apogee is:
KEpKEa=(1+e1−e)2
The distances from the sun to the planet at perigee (rp) and apogee (ra) can be expressed in terms of the semi-major axis a and the eccentricity e:
- At perigee:
rp=a(1−e)
- At apogee:
ra=a(1+e)
The angular momentum L of the planet is conserved. Therefore, we can write:
L=m⋅vp⋅rp=m⋅va⋅ra
where vp is the velocity at perigee and va is the velocity at apogee.
From the conservation of angular momentum, we can derive the ratio of the velocities:
vpva=rarp
Substituting the expressions for rp and ra:
vpva=a(1+e)a(1−e)=1+e1−e
The kinetic energy KE is given by:
KE=12mv2
Thus, the ratio of the kinetic energies at perigee and apogee is:
KEpKEa=12mv2p12mv2a=v2pv2a
Substituting the velocity ratio:
KEpKEa=(vpva)2=(1+e1−e)2
Thus, the ratio of the kinetic energy of the planet at perigee to that at apogee is:
KEpKEa=(1+e1−e)2
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
52 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)
49 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
Knowledge Check
When the earth revolves round the sun in an elliptical orbit, its kinetic energy is
Ago on decreasing continuouslyBgreatest when it is closest to the sunCgreatest when it is farthest from the sunDconstant at all point on the orbitThe ratio of kinetic energy of an electron in Bohr's orbit to its total energy in the same orbit is ______
A−1B2C12D−0.5What is the ratio of the rolling kinetic energy and rotational kinetic energy in the motion of a disc ?
A1:1B2:7C1:2D3:1
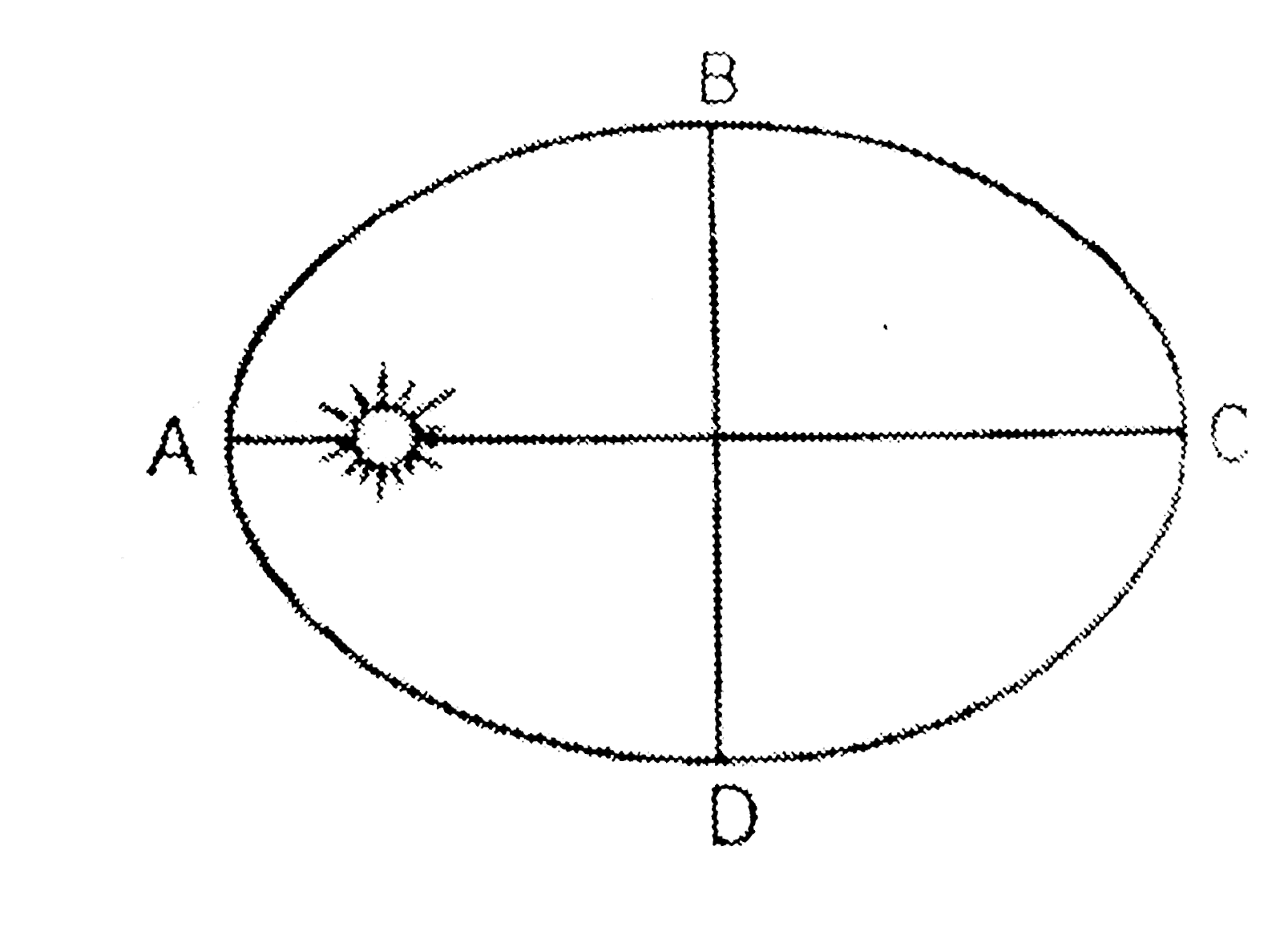
In adjoining figure earth goes around the sun in eliptical orbit on which point the orbital speed is maximum :
View SolutionWho explain the motion of planets around the sun?
View SolutionFor motiion of planets in ellipticla orbits around the sun the central force is
View SolutionA planet revolves around the sun in an elliptical orbit. If vp and va are the velocities of the planet at the perigee and apogee respectively, then the eccentricity of the elliptical orbit is given by :
View SolutionSTATEMENT -1 : If a body is projected from a satellite so as to escape then its velocity of projection with respect to the satellite depends upon the direction of projection.
STATEMENT -2 : Speed of a planet revolving around the sun in an elliptical orbit is maximum at perigee and minimum at apogee.
STATEMENT - 3 : Gravitational field is conservative in nature.
View Solution