A liquid having coefficient of viscosity 0.02 decapoise is filled in a container of cross-sectional area 20 m^2 viscous drag between two adjacent layers in flowing is 1 N, then velocity gradient is
2.0s−1
2.5s−1
3.0s−1
3.5s−1
To solve the problem, we will use the relationship between viscous drag, coefficient of viscosity, area, and velocity gradient. The formula we will use is:
F=μ⋅A⋅dvdx
Where:
- F is the viscous drag (1 N)
- μ is the coefficient of viscosity (0.02 decapoise)
- A is the cross-sectional area (20 m²)
- dvdx is the velocity gradient (what we need to find)
1. Identify the given values:
- Coefficient of viscosity, μ=0.02 decapoise
- Viscous drag, F=1 N
- Cross-sectional area, A=20 m²
2. Convert the coefficient of viscosity to SI units:
- 1 decapoise = 0.1 Pa·s, therefore:
μ=0.02dcP=0.02×0.1Pa⋅s=0.002Pa⋅s
3. Rearrange the formula to solve for the velocity gradient dvdx:
dvdx=Fμ⋅A
4. Substitute the known values into the equation:
dvdx=1N0.002Pa⋅s⋅20m2
5. Calculate the denominator:
0.002Pa⋅s⋅20m2=0.04Pa⋅s⋅m2
6. Now calculate dvdx:
dvdx=1N0.04Pa⋅s⋅m2=25s−1
Final Answer:
The velocity gradient dvdx is 25s−1.
- F is the viscous drag (1 N)
- μ is the coefficient of viscosity (0.02 decapoise)
- A is the cross-sectional area (20 m²)
- dvdx is the velocity gradient (what we need to find)
- Coefficient of viscosity, μ=0.02 decapoise
- Viscous drag, F=1 N
- Cross-sectional area, A=20 m²
- 1 decapoise = 0.1 Pa·s, therefore:
μ=0.02dcP=0.02×0.1Pa⋅s=0.002Pa⋅s
dvdx=Fμ⋅A
dvdx=1N0.002Pa⋅s⋅20m2
0.002Pa⋅s⋅20m2=0.04Pa⋅s⋅m2
dvdx=1N0.04Pa⋅s⋅m2=25s−1
The velocity gradient dvdx is 25s−1.
Similar Questions
The relative velocity of two parallel layers of water is 8 cm/sec. If the perpendicular distance between the layers is 0.1 cm, then velocity gradient will be
View SolutionA liquid of density 103kgm3 and coefficient of viscosity 8 xx10^(-2) decapoise is flowing in a tube of radius 2 cm with speed 2 m/s. The. Reynold’s number is
View Solution
Knowledge Check
A liquid whose coefficient of viscosity is η flows on a horizontal surface. Let dx represent the vertical distance between two layers of liquid and dv represent the difference in the velocities of the two layers. Then the quantity η(dv/dx) has the same dimensions as:
AAccelerationBForceCMomentumDPressureWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical volume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2) , where v0=PR24nl
∴ Q=πPR48stal
This is called Poisecuille's equation .

The velocity of flow of liquid at r = R/2 isA3PR216ηlBPR28ηlCPR24ηlDPR22ηlWhen a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical vloume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2), where v0=PR24nl
∴ Q=πPR48stal

This is called Poisecuille's equation .
The volume of the liquid flowing per sec across the cross - section of the tube is .AπR2v0B(πR2v0)/2C(πR2v0)/3D(πR2v0)/4
When a viscous liquid flows , adjacent layers oppose their relative motion by applying a viscous force given by
F=−ηAdvdz
where , ete = coefficient of viscosity ,
A = surface area of adjacent layers in contact ,
dvdz = velocity gradient
Now , a viscous liquid having coefficient of viscosity η is flowing through a fixed tube of length l and radius R under a pressure difference P between the two ends of the tube . Now consider a cylindrical vloume of liquid of radius r . Due to steady flow , net force on the liquid in cylindrical volume should be zero .
−η2πrldvdr=Pπr2
−∫0v,dv=P2ηl∫Rτrdr(∵ layer in contact with the tube is stationary )
v=v0(1−r2R2), where v0=PR24nl
∴ Q=πPR48stal
This is called Poisecuille's equation .

The viscous force on the cylindrical volume of the liquid varies as
View SolutionAn incompressible liquid flows through a uniform cross section tube with velocity 12 cm/s. the thickness of liquid layer is 0.8 cm then velocity of gradient of flow is
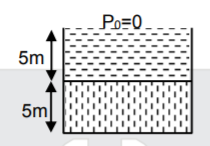
View SolutionTwo liquid columns of same height 5m and densities ρ and 2ρ are filled in a container of uniform cross sectional area. Then ratio of force exerted by the liquid on upper half of the wall to lower half of the wall is.
View SolutionBlood is flowing at the rates of 200 cm3/sec in a capillary of cross-sectional area 0.5m2. The velocity of flow, (in mm/sec) is:
View SolutionAn organic liquid rises 2.0 cm in a capillary tube. How much will it rise if the cross-sectional area of the tube is doubled?
View Solution
