A barometer tube reads 75 cm of Hg. If tube is : gradually inclined at an angle of with horizontal, keeping the open end in the mercury container, then find the length of mercury column in the barometer ■ tube
86.7 cm
150 cm
75 cm
92.5 cm
To solve the problem of finding the length of the mercury column in an inclined barometer tube, we can follow these steps:
1. Understand the Given Information:
- The height of the mercury column in the vertical position is given as H=75cm.
- The barometer tube is inclined at an angle of θ=30∘ with the horizontal.
2. Identify the Relationship:
- When the tube is inclined, the length of the mercury column x in the tube will be longer than the vertical height H due to the inclination. The vertical height of the mercury column remains the same, but the actual length of the mercury column in the tube increases.
3. Use Trigonometry:
- The vertical height H can be related to the length x of the mercury column using the sine function:
H=xsin(θ)
- Rearranging this gives:
x=Hsin(θ)
4. Substitute the Values:
- Substitute H=75cm and θ=30∘:
x=75cmsin(30∘)
5. Calculate sin(30∘):
- We know that sin(30∘)=12.
6. Final Calculation:
- Substitute sin(30∘) into the equation:
x=75cm12=75cm×2=150cm
7. Conclusion:
- The length of the mercury column in the inclined barometer tube is x=150cm.
Summary of the Solution:
The length of the mercury column in the inclined barometer tube is 150cm.
---
- The height of the mercury column in the vertical position is given as H=75cm.
- The barometer tube is inclined at an angle of θ=30∘ with the horizontal.
- When the tube is inclined, the length of the mercury column x in the tube will be longer than the vertical height H due to the inclination. The vertical height of the mercury column remains the same, but the actual length of the mercury column in the tube increases.
- The vertical height H can be related to the length x of the mercury column using the sine function:
H=xsin(θ)
- Rearranging this gives:
x=Hsin(θ)
- Substitute H=75cm and θ=30∘:
x=75cmsin(30∘)
- We know that sin(30∘)=12.
- Substitute sin(30∘) into the equation:
x=75cm12=75cm×2=150cm
- The length of the mercury column in the inclined barometer tube is x=150cm.
The length of the mercury column in the inclined barometer tube is 150cm.
Similar Questions
A barometer tube reads 76 cm of mercury. IFF the tube is gradually inclined keeping the open end immersed in the mercury reservoir, will the length of mercury column be 76 cm, more than 76 cm or less than 76 cm?
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View Solution
Knowledge Check
A barometer tube reads 76 cm of mercury. If the tube is gradually inclined at an angle of 60∘ with vertical, keeping the open end immersed in the mercury reservoir, the length of the mercury column will be
A152cmB76cmC38cmD38√3cmA mercury barometer reads 75cm in vertical position . If the tube is inclined by 60∘ to the vertical, the length of the mercury in the tube will be
A37.5 cmB75cmC112.5cmD150cmIn a mercury barometer, if the tube containing mercury is tilted, then
Aheight of mercury column remains same.Bthe length of mercury column in the tube increses.Cthe vertical height of the mercury column decreases.DBoth (a) and (b)
What will happen if water is used in place of mercury in a barometer tube?
View SolutionCalculate the length of mercury column in a barometer tube which is inclined at an angle of 45∘ with horizontal direction if the atmospheric pressure is 75 cm of mercury.
View SolutionIn given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)
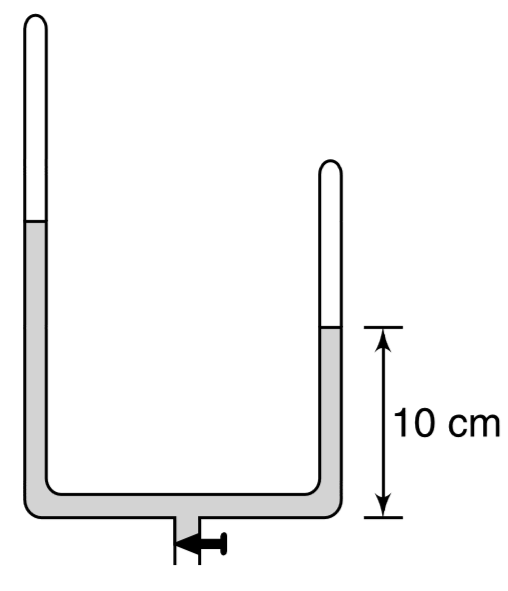
View SolutionA U shaped tube has two arms of equal cross section and lengths l1=80 cm and l2=40 cm. The open ends are sealed with air in the tube at a pressure of 80 cm of mercury. Some mercury is now introduced in the tube through a stopcock connected at the bottom (the air is not allowed to leak out). In steady condition the length of mercury column in the shorter arm was found to be 10 cm. Find the length of the mercury column in the longer arm. Neglect the volume of the part of the tube connecting two arms and assume that the temperature is constant.
View SolutionA tube 1.5 m long and closed at on end is half filled with mercry and is then inverted with its open ends just dipping into a mercury tough.Find the height of mercury in the tube if the reading of the barometer is 0.75 m.
View Solution
