A vertical U-tube of uniform cross-section contains water jn both the arms. A 10 cm glycerine column (R.D. = 1.2) is added to one of the limbs. The level difference between the two free surfaces in the two limbs wiil be
4cm
2cm
6cm
8cm
To solve the problem of finding the level difference between the two free surfaces in a vertical U-tube after adding a 10 cm glycerin column (with a relative density of 1.2) to one of the limbs, we can follow these steps:
1. Understand the Setup:
- We have a U-tube with water in both arms initially at the same level.
- A 10 cm column of glycerin is added to one limb.
2. Identify the Densities:
- The relative density (R.D.) of glycerin is given as 1.2.
- The density of water (ρ_w) is approximately 1000 kg/m³.
- Therefore, the density of glycerin (ρ_g) can be calculated as:
ρg=R.D.×ρw=1.2×1000kg/m3=1200kg/m3
3. Set Up the Pressure Balance:
- The pressure difference due to the glycerin column must be balanced by the pressure difference in the water column on the other side.
- Let x be the height difference in water levels in the two arms after adding glycerin.
4. Calculate the Pressure from Glycerin:
- The pressure exerted by the glycerin column is given by:
Pg=ρg⋅g⋅hg=1200kg/m3⋅g⋅0.1m=120kg/m2⋅g
- Here, hg=10cm=0.1m.
5. Calculate the Pressure from Water:
- The pressure exerted by the water column on the other side is:
Pw=ρw⋅g⋅(10cm+x)=1000kg/m3⋅g⋅(0.1+x100)m
6. Set the Pressures Equal:
- Since the pressures must balance, we can set up the equation:
120g=1000⋅(0.1+x100)⋅g
- The g cancels out:
120=1000⋅(0.1+x100)
7. Solve for x:
- Simplifying the equation:
120=100+10x
20=10x
x=2cm
8. Conclusion:
- The level difference between the two free surfaces in the two limbs of the U-tube is 2cm.
Final Answer:
The level difference between the two free surfaces in the two limbs will be 2 cm.
- We have a U-tube with water in both arms initially at the same level.
- A 10 cm column of glycerin is added to one limb.
- The relative density (R.D.) of glycerin is given as 1.2.
- The density of water (ρ_w) is approximately 1000 kg/m³.
- Therefore, the density of glycerin (ρ_g) can be calculated as:
ρg=R.D.×ρw=1.2×1000kg/m3=1200kg/m3
- The pressure difference due to the glycerin column must be balanced by the pressure difference in the water column on the other side.
- Let x be the height difference in water levels in the two arms after adding glycerin.
- The pressure exerted by the glycerin column is given by:
Pg=ρg⋅g⋅hg=1200kg/m3⋅g⋅0.1m=120kg/m2⋅g
- Here, hg=10cm=0.1m.
- The pressure exerted by the water column on the other side is:
Pw=ρw⋅g⋅(10cm+x)=1000kg/m3⋅g⋅(0.1+x100)m
- Since the pressures must balance, we can set up the equation:
120g=1000⋅(0.1+x100)⋅g
- The g cancels out:
120=1000⋅(0.1+x100)
- Simplifying the equation:
120=100+10x
20=10x
x=2cm
- The level difference between the two free surfaces in the two limbs of the U-tube is 2cm.
The level difference between the two free surfaces in the two limbs will be 2 cm.
Similar Questions
A vertical U - tube of uniform cross - section contains water in both the arms. A 10 cm glycerine column (R.D. = 1.2) is added to one of the limbs. What is the level difference between the two free surface in the two limbs?
View SolutionA vertical U tube of uniform cross section contains mercury in both of its arms. A glycerine (d=1.3g/cm3) column of length 10cm is introduced into one of the arms. Oil of density 0.8g/cm3 is poured in the other arm until the upper surfaces of the oil and glycerine are in the same horizontal level. Find the length of oil column. Densit of mercury is 13.6g/cm3.

View Solution
Knowledge Check
Fig, shows a U-tube of uniform cross-sectional area A accelerated with acceleration a as shown. If d is the seperation between the limbs. Then the difference in the levels of the liquid in the U−tube is
 AadgBgadCadgDad+g
AadgBgadCadgDad+gA bent tube of uniform cross section is mounted on a cart which is accelerating towards right with constant acceleration 'a'. The total length of the liquid is 2√2l. Find the level difference between two limbs in equilibrium (a=2m/s2,l=10m)
 A2 mB4 mC6 mD12 m
A2 mB4 mC6 mD12 m
_S01_015_Q01.png)
A vertical U-tube of uniform cross-section contains mercury in both arms A glycerine (relative density =1.3) column of length 10 cm is introduced into one of the arms. Oil of density 800 gm m−3 is poured into the other arm until the upper surface of the oil and hlycerine are at the same horizontal level, find the length of the column. Density of mercury is 13.6×103kgm−3
View SolutionA vertical U-tube of uniform inner cross-section contains mercury in both of its arms. A glycerine (density1.3gcm−3) column of length 10cmis introduced into one of the arms Oil of density 0.8gcm−3 is poured in the other arm until the upper surface of the oil and glycerine are in the same horizontal level. Find the length of the oil column.
View SolutionA vertical U-tube of uniform cross-section contains water upto a height of 30 cm. show that if the water in one limb is depressed and then released, its up and down motion in the two limbs of the tube is simple harmonic and calculate its time-period.
View SolutionA vertical U-tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density =1.3g/cm3) column of length 10 cm is introduced into one of its arms. Oil of density 0.8 gm/cm3 is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the same horizontal level. Find the length of the oil column, Density of mercury =13.6g/cm3
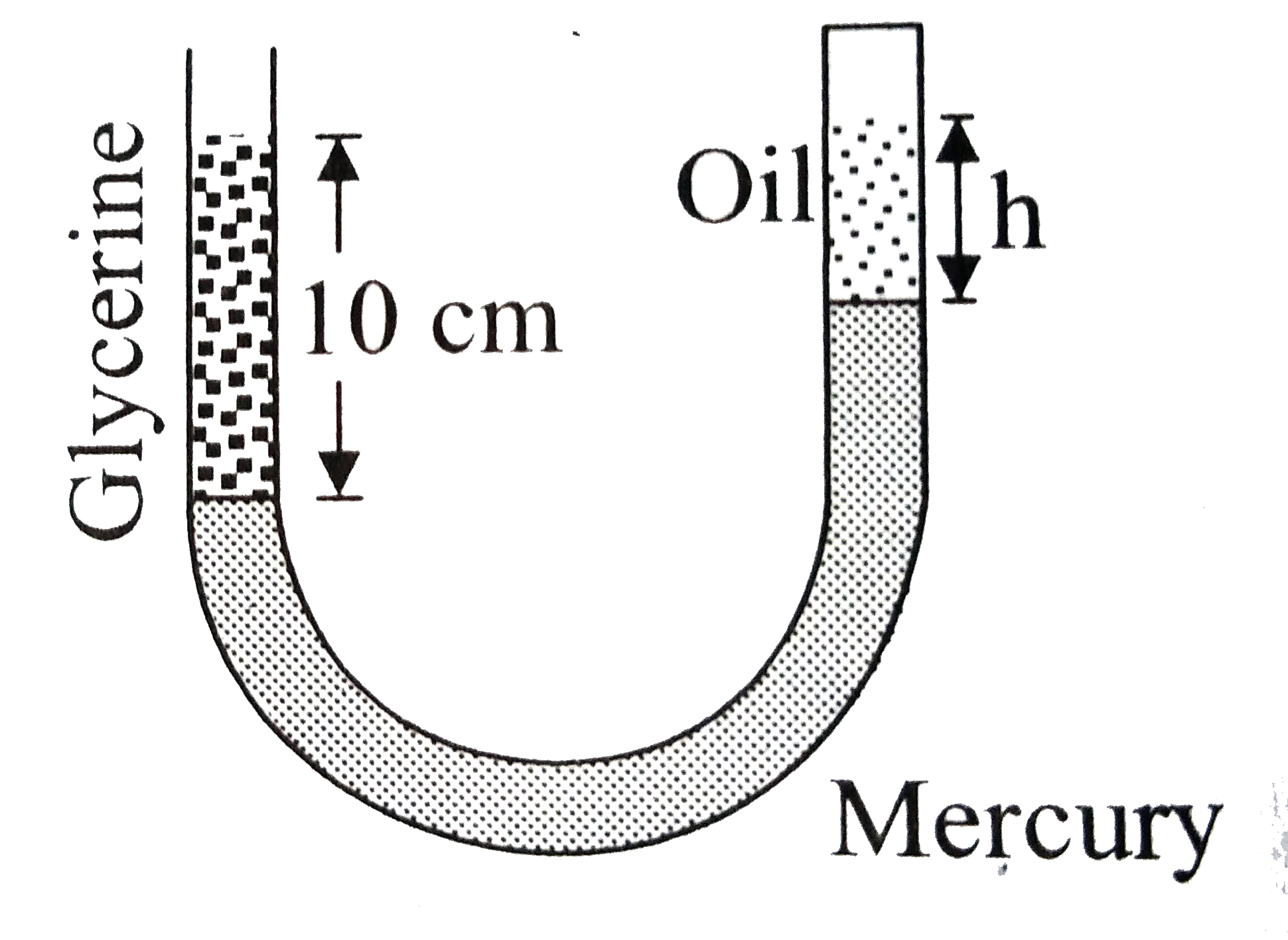
View SolutionA vertical U tube of uniform cross-section contains water up to a heigth of 0.5m . If water on one side is depressed a little and then released its motino up and down the two sides of the tube is SHM. Calculate (i) time period (ii) angular grequency of vibration. g=10ms2.
View SolutionA vertical U-tube of uniform cross-section contains water upto a height of 30 cm. show that if the water in one limb is depressed and then released, its up and down motion in the two limbs of the tube is simple harmonic and calculate its time-period.
View Solution
