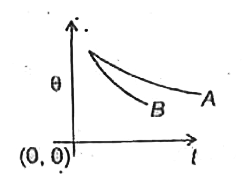
Two bodies A and B of same mass, area and surface finish with specific heats $S_{A}$ and $S_{B}$ $(S_{A} > S_{B})$ are allowed to cool for given temperature range. Temperature varies with time as

ocr_image

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to analyze the cooling rates of two bodies A and B based on their specific heats. Here's a step-by-step breakdown of the solution:
Step 1: Understand the Given Information
We have two bodies, A and B, with:
- Same mass (m)
- Same surface area (A)
- Same surface finish
- Specific heats: $S_{A} > S_{B}$
Step 2: Apply Newton's Law of Cooling
According to Newton's Law of Cooling, the rate of change of temperature of a body is proportional to the difference in temperature between the body and its surroundings. Mathematically, this can be expressed as:
$\frac{d θ}{d t} \propto - (θ - θ_{a m b i e n t})$
Where:
- $θ$ is the temperature of the body
- $θ_{a m b i e n t}$ is the ambient temperature
Step 3: Relate Cooling Rate to Specific Heat
The rate of cooling (i.e., the rate of change of temperature) is inversely proportional to the specific heat of the body. This means:
\frac{d\theta_A}{dt} < \frac{d\theta_B}{dt} \quad \text{(since S_A > S_B )}
This implies that body A, with a higher specific heat, will cool down more slowly than body B.
Step 4: Compare the Cooling Curves
At any given time $t$ , since body A cools down slower than body B, we can conclude:
$θ_{A} (t) > θ_{B} (t)$
This means that at any instant during the cooling process, the temperature of body A will be greater than that of body B.
Step 5: Graphical Representation
When we plot the cooling curves of both bodies:
- The curve for body A will be above the curve for body B at all times.
- Both curves will start at the same initial temperature and will decrease over time, but the curve for A will decrease less steeply than that for B.
Conclusion
The correct option will show that the temperature of body A is always greater than that of body B during the cooling process.
Final Answer
The cooling curve of body A will always be above that of body B, confirming that $θ_{A} > θ_{B}$ at all times during the cooling process.
---

Updated on:7/8/2024

Radius of a shere is $R$ density is d and specific heat is s, Is is heated and then allowed to cool Its rate of decrease of temperature will be proportional to .
A $R d s$
B $1 / R d s$
C $1 / R^{2} d s$
D $R^{2} d s$
There are two spherical balls A and B of the same material with same surface, but the diameter of A is half that of B . If A and B are heated to the same temperature and then allowed to cool, then
ARate of cooling is same in both
BRate of cooling of A is four times that of B
CRate of cooling of A is twice that of B
DRate of cooling of A is $\frac{1}{4}$ times that of B
Two bodies A and B have the same surface area and mass the bodies have absolute temperatures $T_{A} and T_{B}$ emissivities $e_{a}$ and $e_{b}$ and specific heat capacities $s_{A}$ and $s_{B}$ . The intensity, E , of radiation near a given wavelength is shown plotted against the wavelength $λ$ , of radiation for both the bodies. Which of the following is possible?
A $T_{A} = T_{B}, e_{A} = e_{B}, s_{A} \neq s_{B}$
B $T_{A} = T_{B}, e_{A} \neq e_{B}, s_{A} = s_{B}$
C $T_{A} \neq T_{B}, e_{A} = e_{B}, s_{A} = s_{B}$
D $T_{A} \neq T_{B}, e_{A} = e_{B}, s_{A} \neq s_{B}$