If the particle repeats its motion after a fixed time interval of 8 s then after how much time its maximum value of PE will be attained after attaining its minimum value ?
2s
4s
8s
1s
The correct Answer is:A
To solve the problem, we need to understand the relationship between the potential energy (PE) and the position of the particle in oscillatory motion. The potential energy in a simple harmonic oscillator is maximum when the particle is at the extreme positions (maximum displacement) and minimum when the particle is at the mean position (equilibrium position).
1. Identify the Period of Motion:
The problem states that the particle repeats its motion after a fixed time interval of 8 seconds. This time interval is the period (T) of the oscillation.
T=8 seconds
2. Determine the Time for Maximum and Minimum PE:
In one complete cycle of oscillation:
- The potential energy is minimum when the particle is at the mean position (x = 0).
- The potential energy is maximum when the particle is at the extreme positions (x = ±A, where A is the amplitude).
3. Analyze the Motion:
- At t=0, assume the particle is at the mean position (minimum PE).
- The particle will take a quarter of the period (T/4) to reach the maximum displacement (maximum PE).
4. Calculate Time to Maximum PE:
Since the period T is 8 seconds, we calculate T/4:
T4=8 seconds4=2 seconds
5. Conclusion:
Therefore, after attaining its minimum value of potential energy, the maximum value of potential energy will be attained after 2 seconds.
Final Answer:
The maximum value of potential energy will be attained after 2 seconds.
---
The problem states that the particle repeats its motion after a fixed time interval of 8 seconds. This time interval is the period (T) of the oscillation.
T=8 seconds
In one complete cycle of oscillation:
- The potential energy is minimum when the particle is at the mean position (x = 0).
- The potential energy is maximum when the particle is at the extreme positions (x = ±A, where A is the amplitude).
- At t=0, assume the particle is at the mean position (minimum PE).
- The particle will take a quarter of the period (T/4) to reach the maximum displacement (maximum PE).
Since the period T is 8 seconds, we calculate T/4:
T4=8 seconds4=2 seconds
Therefore, after attaining its minimum value of potential energy, the maximum value of potential energy will be attained after 2 seconds.
The maximum value of potential energy will be attained after 2 seconds.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section C) (PREVIOUS YEARS QUESTIONS)43videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)13videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section - A) (OBJECTIVE TYPE QUESTIONS)60videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)5videos
PHYSICAL WORLD
Similar Questions
Knowledge Check
- Question 1 - Select One
The electric current that reverses its direction after a fix interval of time, is called
Adirect currentBinduced currentCalternating currentDelectromagnetic current - Question 2 - Select One
The equation E= cos x.sinx attains its maximum value at x=
Aπ3Bπ4Cπ2Dnone of these - Question 3 - Select One
the time after which the particle attains maximum height is :
A12√3sB√32sC2√3sD1s
A particle executing simple harmonic motion has a time period of 4 s. If the particle starts moving from the mean position at t = 0, then after how much interval of time from t = 0, will its displacement be half of its amplitude ?
View SolutionA particle starting from rest undergoes a rectilinear motion with acceleration a. The variation of a with time t is shown below. The maximum velocity attained by the particle during its motion is
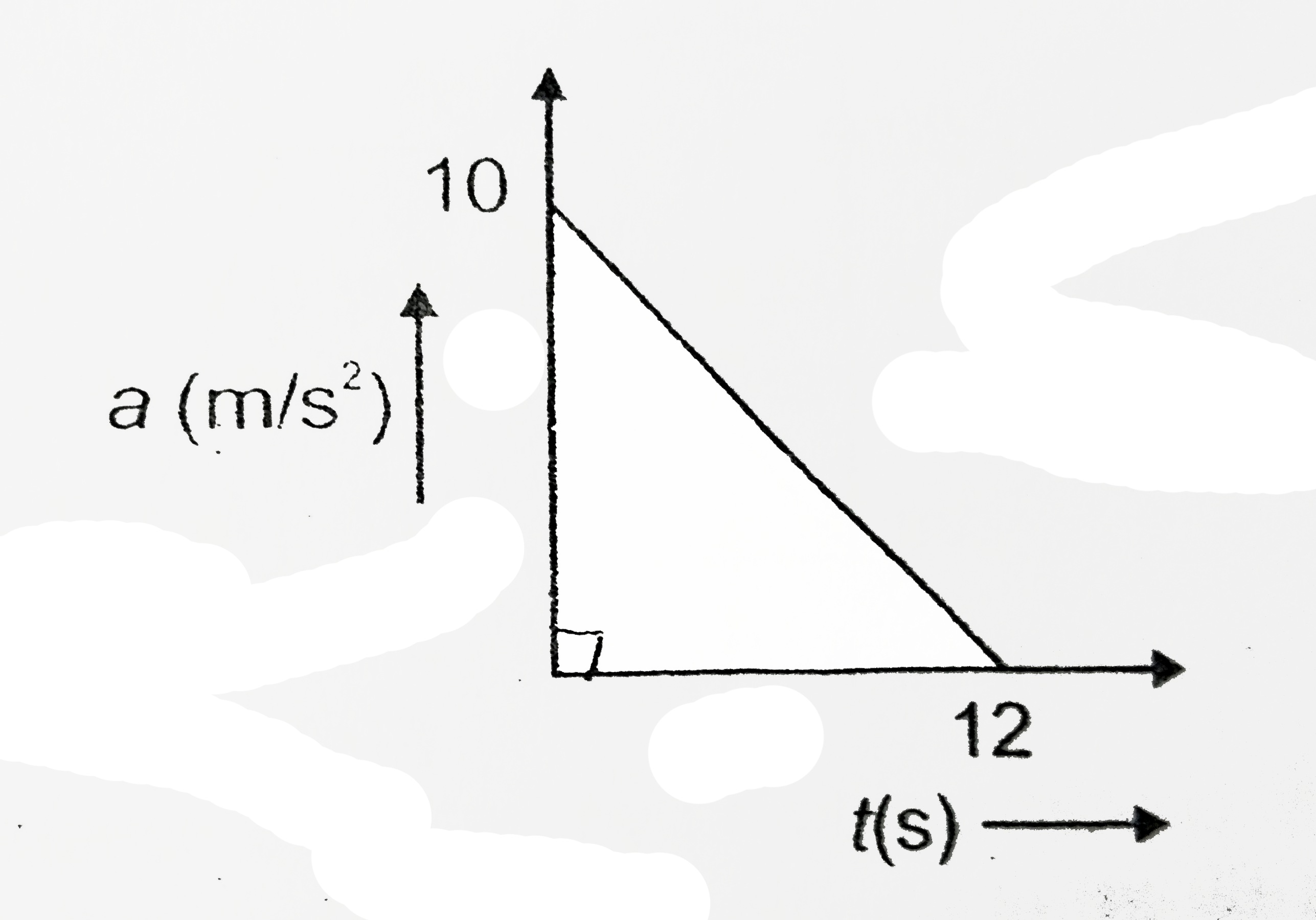 View Solution
View SolutionDraw a velocity versus time graph of a stone thrown vertically upwards and then coming downwards after attaining the maximum height .
View SolutionFind the time after which current in the circuit becomes 80% of its maximum value
View SolutionThe number of values of x where f(x) = cosx+cos√2 x attains its maximum value is
View Solution

