Masses MAandMB hanging from the ends of strings of lengths LAandLB are executing simple harmonic motions. If their frequencies are fA=2fB, then
lA=lB4, does not depend on mass
lA=4lB, does not depend on mass
lA=2lBandMA=2MB
lA=lB2andMA=MB2
The correct Answer is:A
Step by step video, text & image solution for Masses M_(A) "and" M_(B) hanging from the ends of strings of lengths L_(A) "and" L_(B) are executing simple harmonic motions. If their frequencies are f_(A) = 2f_(B), then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)13videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section - B) (OBJECTIVE TYPE QUESTIONS)30videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)5videos
PHYSICAL WORLD
Similar Questions
" The frequency of a particle executing simple harmonic motion is 'f' hertz.The frequency of variation of its kinetic energy is "
View Solution(a) Derive an expression for the energy of a particle executing simple harmonic motion.
(b) The length of a simple pendulum in increased by 15%. What will be the percentage increase in time period ?View Solution
Knowledge Check
- Question 1 - Select One
Two bodies of mass m and 4m are attached by a string shown in the figure-2.146. The body of mass m hanging from a string of length l is executing simple harmonic motion with amplitude A while other body is at rest on the surface. The minimum coefficient of friction between the mass 4m and the horizontal surface must be to keep it at rest is :
 A14(1−A2l2)B14(1+A2l2)C14AlcosθD14
A14(1−A2l2)B14(1+A2l2)C14AlcosθD14 - Question 2 - Select One
A particle executes simple harmonic motion with a frequency f. The frequency with which its kinetic energy oscillates is
Af// 2BfC2 fD4 f - Question 3 - Select One
A particle executes simple harmonic motion with a frequency f. The frequency with which the potential. Energy oscillates is
AfBf/2C2fDzero
A particle executes simple harmonic motion with a frequency f. The frequency with which its kinetic energy oscillates is
View SolutionA particle of mass m moving along x-axis has a potential energy U(x)=a+bx2 where a and b are positive constant. It will execute simple harmonic motion with a frequency determined by the value of
View SolutionA pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
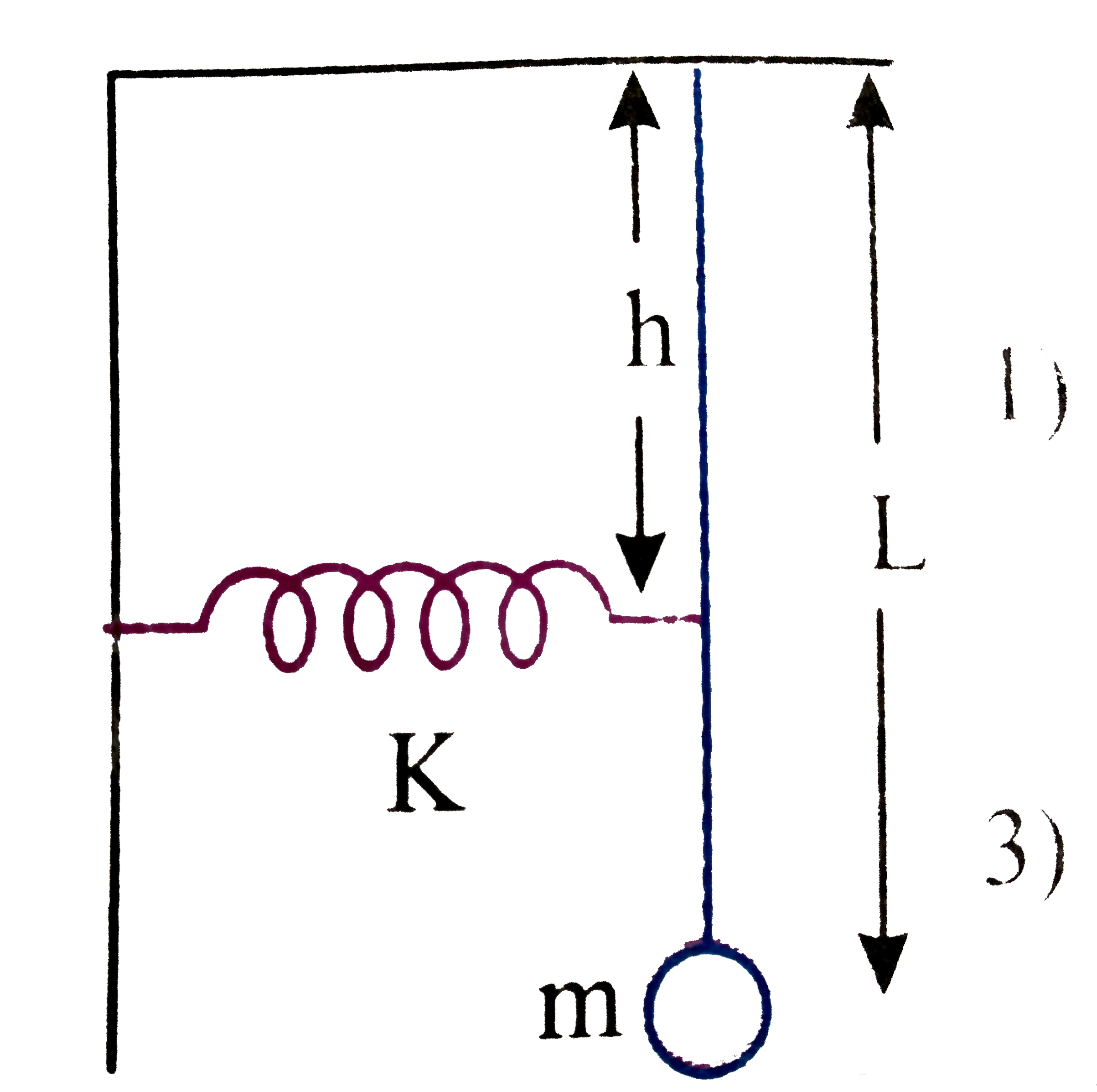 View Solution
View SolutionUnder the action of load F1, the length of a string is L1 and that under F2, is L2. The original length of the wire is
View SolutionThe masses and length of two simple pendulums are given as respectively mA,mB,LAandLB. If frequency of A is double that of B then relation between LAandlB is given as
View Solution

