A: If a spring block system, oscillating in a vertical plane is made to oscillate on a horizontal surface, the time period will remain same.
R: The time period of spring block system does not depend on g.
If both Assertion & Reason are true and the reason is the correct explanation of the assertion, then mark (1)
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark (2)
If Assertion is true statement but Reason is false then mark (3)
If both Assertion and Reason are false statements, then mark (4)
The correct Answer is:B
To analyze the statements given in the question, we need to evaluate both the Assertion (A) and the Reason (R) regarding the time period of a spring-block system.
Step 1: Understanding the Time Period of a Spring-Block System
The time period (T) of a spring-block system is given by the formula:
T=2π√mk
where:
- m is the mass of the block,
- k is the spring constant.
Step 2: Analyzing the Assertion (A)
The assertion states that if a spring-block system oscillating in a vertical plane is made to oscillate on a horizontal surface, the time period will remain the same.
- When the system oscillates vertically, the gravitational force affects the equilibrium position of the spring but does not affect the time period of oscillation.
- When the system is moved to a horizontal surface, the gravitational force does not influence the oscillation since the spring's restoring force is still determined by the displacement from the equilibrium position.
Thus, the assertion (A) is true.
Step 3: Analyzing the Reason (R)
The reason states that the time period of a spring-block system does not depend on g (acceleration due to gravity).
- From the formula for the time period, we can see that g does not appear in the equation.
- This indicates that the time period is independent of gravitational acceleration, confirming that the time period is solely dependent on mass and spring constant.
Thus, the reason (R) is also true.
Step 4: Conclusion
Since both the assertion (A) and the reason (R) are true, and the reason correctly explains the assertion, we conclude that:
- The assertion is true, and the reason is true, and the reason is a correct explanation of the assertion.
Final Answer:
Both A and R are true, and R is the correct explanation of A.
---
The time period (T) of a spring-block system is given by the formula:
T=2π√mk
where:
- m is the mass of the block,
- k is the spring constant.
The assertion states that if a spring-block system oscillating in a vertical plane is made to oscillate on a horizontal surface, the time period will remain the same.
- When the system is moved to a horizontal surface, the gravitational force does not influence the oscillation since the spring's restoring force is still determined by the displacement from the equilibrium position.
The reason states that the time period of a spring-block system does not depend on g (acceleration due to gravity).
- This indicates that the time period is independent of gravitational acceleration, confirming that the time period is solely dependent on mass and spring constant.
Since both the assertion (A) and the reason (R) are true, and the reason correctly explains the assertion, we conclude that:
- The assertion is true, and the reason is true, and the reason is a correct explanation of the assertion.
Both A and R are true, and R is the correct explanation of A.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Assignment (Section C) (PREVIOUS YEARS QUESTIONS)43videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)5videos
PHYSICAL WORLD
Similar Questions
Knowledge Check
- Question 1 - Select One
Time period of a spring mass system can be changed by
Achanging the massBacclerating the point of suspension of the blockCcutting the spring (i.e.changing the length of the spring)Dimmersing the mass in a liquid - Question 2 - Select One
The two spring-mass system, shown in the figure, oscillates with a period T. If only one spring is used, the time period will be
 AT√2BT2C√2TD2T
AT√2BT2C√2TD2T - Question 3 - Select One
The two spring-mass system, shown in the figure, oscillates with a period T. If only one spring is used, the time period will be
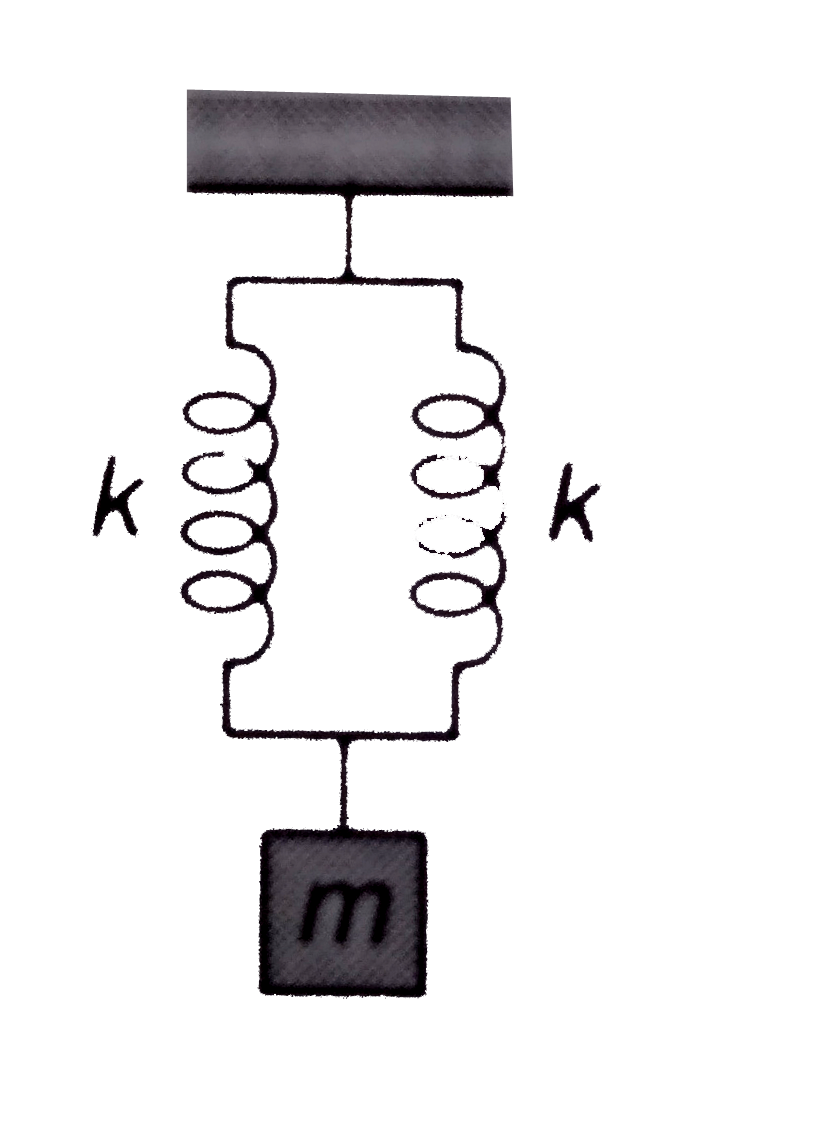 AT√2BT2C√2TD2T
AT√2BT2C√2TD2T
Find time period of oscillation of the system.
 View Solution
View SolutionHow would the period of spring mass system change, when it is made to oscillate horizontally and then vertically?
View SolutionThe time period of oscillation of the block as shown in figure is
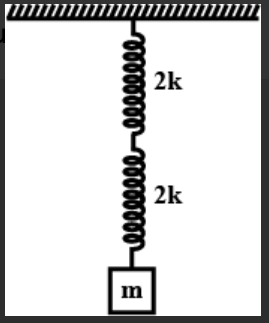 View Solution
View SolutionComparing the L-C oscillations with the oscillations of a spring-block system
View SolutionA spring - block system undergoes vertical oscillation above a large horizontal metal sheet with uniform positive charge. The time period of the oscillation will be is given a charge Q , its time period of oscillation will be
View Solution

