There are two charges +2μC and −3μC. The ratio of forces acting on them will be
(1) 2:3 (2) 1:1
(3) 3:2 (4) 4:9
To find the ratio of forces acting on two charges, we can use Coulomb's law, which states that the force F between two point charges q1 and q2 separated by a distance d is given by:
F=k|q1⋅q2|d2
where k is Coulomb's constant.
1. Identify the Charges: We have two charges, q1=+2μC and q2=−3μC.
2. Calculate the Forces: According to Coulomb's law, the force acting on charge q1 due to charge q2 is:
F12=k|q1⋅q2|d2=k|(2×10−6)⋅(−3×10−6)|d2
Similarly, the force acting on charge q2 due to charge q1 is:
F21=k|q2⋅q1|d2=k|(−3×10−6)⋅(2×10−6)|d2
3. Observe the Magnitudes: The magnitudes of the forces F12 and F21 are equal because they depend on the product of the charges and the distance:
|F12|=|F21|
4. Ratio of Forces: Since the magnitudes of the forces are equal, we can express the ratio of the forces acting on the two charges as:
F12F21=1
5. Final Answer: Therefore, the ratio of the forces acting on the charges +2μC and −3μC is:
Ratio=1:1
Conclusion:
The correct answer is option (2) 1:1.
F12=k|q1⋅q2|d2=k|(2×10−6)⋅(−3×10−6)|d2
Similarly, the force acting on charge q2 due to charge q1 is:
F21=k|q2⋅q1|d2=k|(−3×10−6)⋅(2×10−6)|d2
|F12|=|F21|
F12F21=1
Ratio=1:1
The correct answer is option (2) 1:1.
Similar Questions
Knowledge Check
There are two charges +1μC and−5μC under mutual coulombic interaction . The ratio of magnitude of forces acting on themwill be
A1:5B1:1C5:1D1:25There are two charge +1μc and +2μc kept at certain separartion ,the ratio of electrostatic forces acting on them will be in the ratio
A1:2B2:1C1:1D1:4A metal of surface area 1m2 is charged with √8.85μC in air. The mechanical force acting on it is
A1NB0.5 NC10 ND50N
The force between two charges 9μ C and 1μc separated by a distance 3m in space is..........
View SolutionThe radii of two circles are in the ratio 2: 3. The ratio of their areas is (a) 2:3 (b) 4:9 (c) 3:2 (d) 9:4
View SolutionMatch the following.
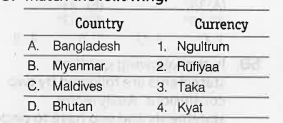
Codes A B C D
(A) 4 3 1 2 (B) 2 4 1 3 (C) 3 4 2 1 (D) 3 4 1 2
View SolutionIf the heights of two cones are in the ratio of 1:4 and the radii of their bases are in the ratio 4:1, then the ratio of their volumes is (a) 1:2 (b) 2:3 (c) 3:4 (d) 4:1
View SolutionA right angled prism of refractive index μ1 is placed in a rectangular block of refractive index μ2 , which is surrounded by a medium of refractive index μ3 ,as shown in the figure . A ray of light 'e' enters the rectangular block at normal incidence . depending upon the relationship between μ1,μ2andμ3 , it takes one of the four possible paths 'ef' , 'eg' , 'eh' or 'ef'
_E01_228_Q01.png)
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists:
{:("List" I , "List" II) , ( P. e rarr f , 1. mu_(1)gt sqrt(2mu_(2))) , ( Q. e rarr g , 2. mu_(2) gt mu_(1) "and" mu_(2) gt mu_(3)), ( R. e rarr f , 3. mu_(1) = mu_(2)), ( S. e rarr f , 4. mu_(2) lt mu_(1) lt sqrt(2mu_(2)) "and" mu_(2) gt mu_(3)):}<br>Codes:<br>{:( P , Q , R , S) , ((A) 2 , 3 , 1 , 4), ((B) 1 , 2 , 4 , 3) , ((C) 4 , 1 , 2 , 3) , ((D) 2, 3 , 4 , 1):}
View Solution
