A point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm. The magnitude of the flux through the square is
ε0
1ε0
ε0×10−6
1ε0×10−6
To solve the problem of finding the electric flux through a square when a point charge is placed above it, we can follow these steps:
1. Identify the Given Data:
- Point charge, Q=+6μC=6×10−6C
- Distance from the charge to the center of the square, d=20cm=0.2m
- Side length of the square, a=40cm=0.4m
2. Visualize the Setup:
- Imagine a cube where the square is one of its faces. The charge is located at the center of this cube.
3. Apply Gauss's Law:
- According to Gauss's Law, the total electric flux Φ through a closed surface is given by:
Φ=Qencϵ0
- Here, Qenc is the charge enclosed by the Gaussian surface (the cube), and ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/(N⋅m2).
4. Calculate the Total Flux through the Cube:
- Since the charge is at the center of the cube, the total flux through the cube is:
Φtotal=6×10−68.85×10−12≈6.78×105N⋅m2/C
5. Determine the Flux through One Face of the Cube:
- The cube has 6 faces, and due to symmetry, the flux through each face is the same. Therefore, the flux through one face (which is the square in question) is:
Φsquare=Φtotal6=6.78×1056≈1.13×105N⋅m2/C
Final Answer:
The magnitude of the electric flux through the square is approximately 1.13×105N⋅m2/C.
---
- Point charge, Q=+6μC=6×10−6C
- Distance from the charge to the center of the square, d=20cm=0.2m
- Side length of the square, a=40cm=0.4m
- Imagine a cube where the square is one of its faces. The charge is located at the center of this cube.
- According to Gauss's Law, the total electric flux Φ through a closed surface is given by:
Φ=Qencϵ0
- Here, Qenc is the charge enclosed by the Gaussian surface (the cube), and ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/(N⋅m2).
- Since the charge is at the center of the cube, the total flux through the cube is:
Φtotal=6×10−68.85×10−12≈6.78×105N⋅m2/C
- The cube has 6 faces, and due to symmetry, the flux through each face is the same. Therefore, the flux through one face (which is the square in question) is:
Φsquare=Φtotal6=6.78×1056≈1.13×105N⋅m2/C
The magnitude of the electric flux through the square is approximately 1.13×105N⋅m2/C.
Similar Questions
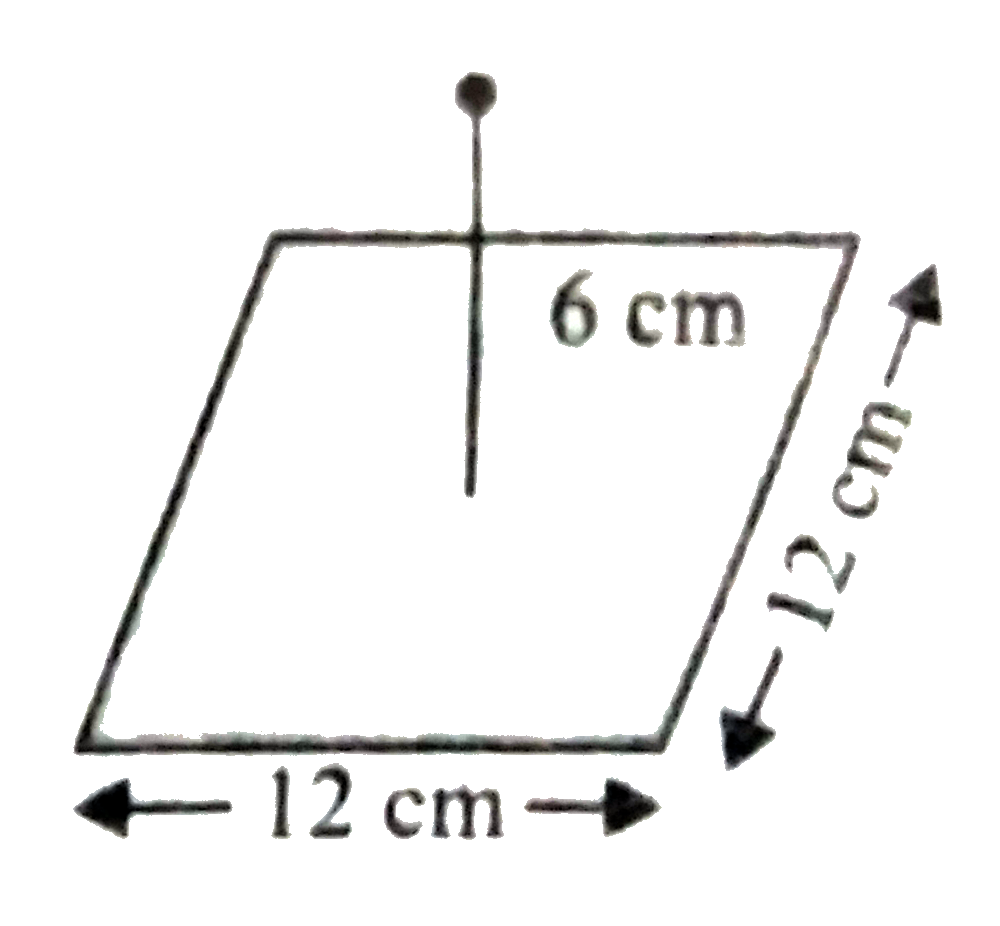
A point charge +20muC is at a distance 6 cm directly above the centre of a square of side 12 cm as shown is figure. The magnitude of electric flux through the square is
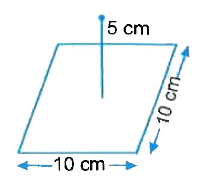
View SolutionA point charges +10μC is a distance 5 cm directly above centre of a square of side 10 cm as shown in What is the magnitude of the electric flux through the square?
View Solution
Knowledge Check
A point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm . The magnitude of the flux through the square is
Aε0B1ε0Cε0×10−6D1ε0×10−6A point charge q is placed at a distance a/2 directly above the center of a square of side a. The electric flux through the square is
Aqε0Bqπε0Cq4ε0Dq6ε0A point charge q is placed at a distance a2 directly above the centre of a horizontal square of side 'a' and another point charge -q is placed at a distance 'a' directly below one of its (the square's) corners. The electric flux through the square is :
Aq6∈0Bq8∈0Cq24∈0D5q24∈0
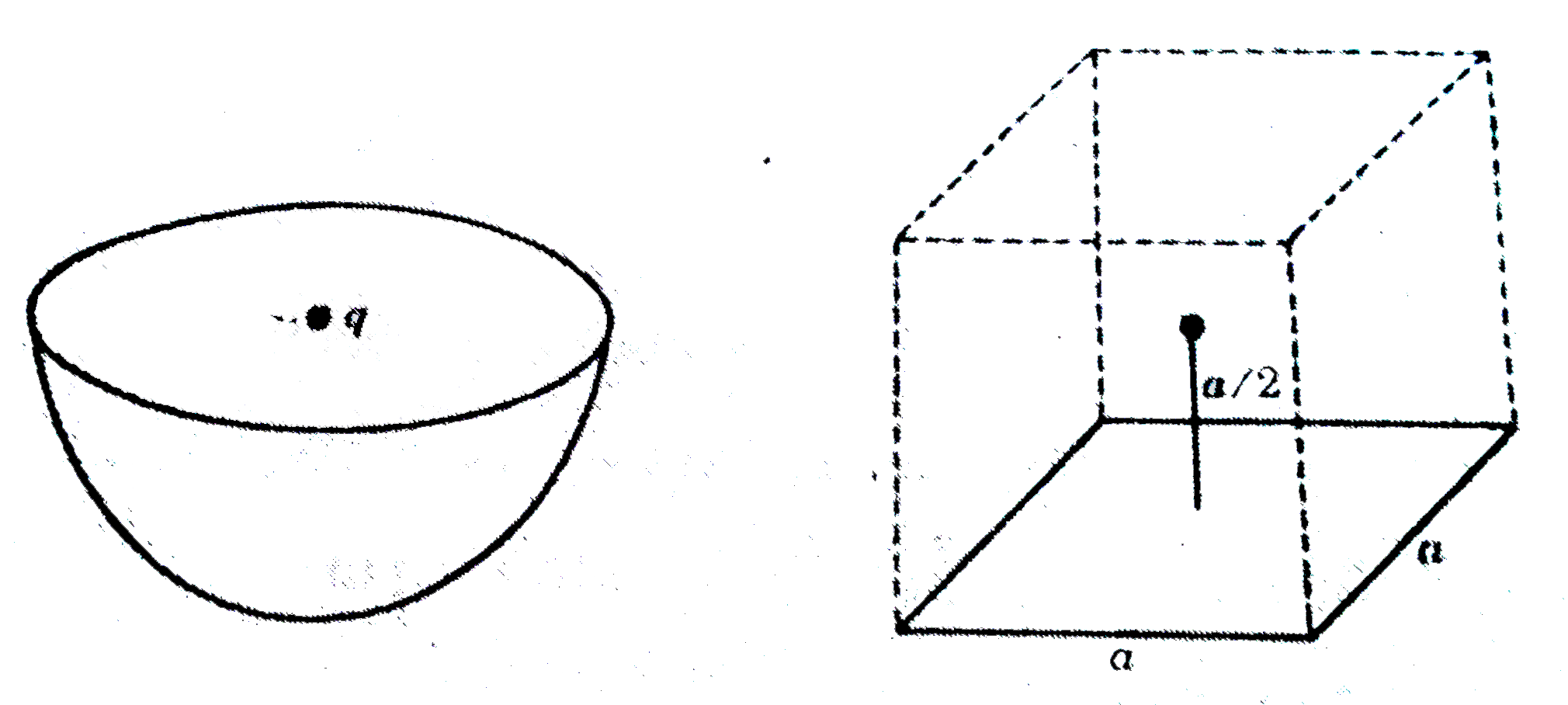
A point charge q is placed at a distnace a/2 directly above the centre of a square of side a, as shown figure. Find the magnitude of the electric flux through the square.
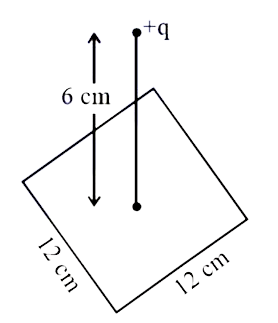
View SolutionA point charge of +12μC is at a distance 6 cm vertically above the centre of a square of side 12 cm as shown in figure. The magnitude of the electric flux through the square will be _______ ×103Nm2/C.
View SolutionA point charge +10μC is at distance of 5cm directly above the center of a square of side 10 cm as shown in Fig. What is the magnitude of the electric flux through the square ? (Hint. Think of the square of the square as one face of a cube with edge 10 cm)
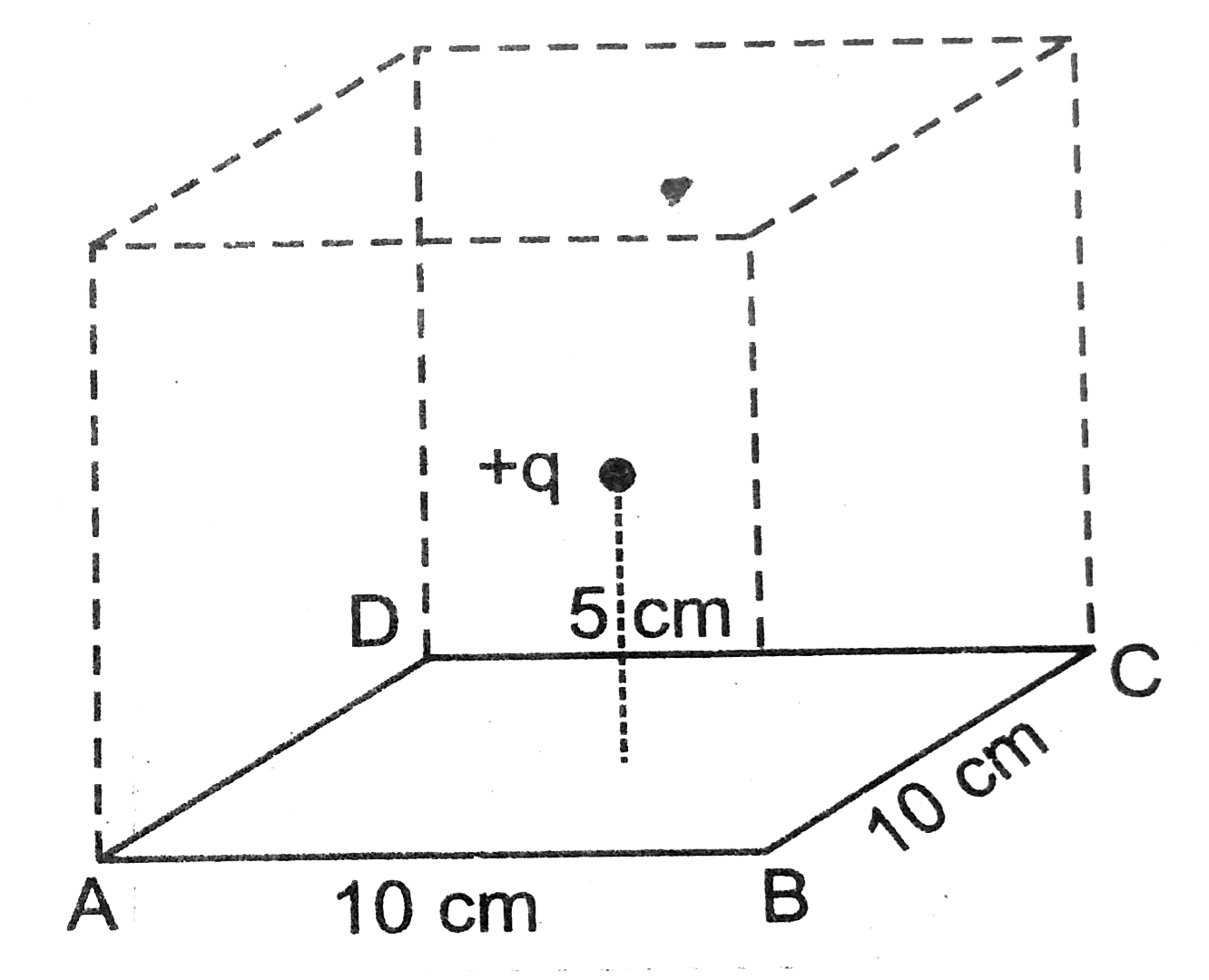
View SolutionA point charge Q is placed at the corner of a square of side a, then find the flux through the square.

View SolutionA point charge Q is placed at the corner of a square of side a. Find the flux through the square.
View Solution
