Electric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
σ2ε0
σε0
σ22ε0
σ2ε0
To find the electric field due to an infinite non-conducting sheet of surface charge density σ at a distance r from it, we can use Gauss's law. Here is a step-by-step solution:
Step 1: Understand the Setup
We have an infinite non-conducting sheet with a uniform surface charge density σ. We want to find the electric field E at a distance r from the sheet.
Step 2: Choose a Gaussian Surface
To apply Gauss's law, we choose a cylindrical Gaussian surface. The axis of the cylinder should be perpendicular to the sheet. The cylinder has two flat surfaces (caps) and a curved surface.
Step 3: Calculate Electric Flux
The electric field E due to the charged sheet will be perpendicular to the surface of the sheet. Therefore, the electric field will be uniform and directed away from the sheet on both sides.
The electric flux Φ through the Gaussian surface is given by:
Φ=∫E⋅dA
Since the electric field is uniform and perpendicular to the area vector on the flat surfaces, we can write:
Φ=E⋅Atop+E⋅Abottom+0=E⋅A+E⋅A=2EA
where A is the area of one of the flat surfaces of the cylinder.
Step 4: Apply Gauss's Law
According to Gauss's law:
Φ=Qencϵ0
where Qenc is the charge enclosed by the Gaussian surface. The charge on the sheet that contributes to the electric field is:
Qenc=σA
Thus, we can write:
2EA=σAϵ0
Step 5: Solve for Electric Field E
Now, we can cancel A from both sides (assuming A≠0):
2E=σϵ0
Therefore, the electric field E is:
E=σ2ϵ0
Conclusion
The electric field due to an infinite non-conducting sheet of surface charge density σ at a distance r from it is:
E=σ2ϵ0
We have an infinite non-conducting sheet with a uniform surface charge density σ. We want to find the electric field E at a distance r from the sheet.
To apply Gauss's law, we choose a cylindrical Gaussian surface. The axis of the cylinder should be perpendicular to the sheet. The cylinder has two flat surfaces (caps) and a curved surface.
The electric field E due to the charged sheet will be perpendicular to the surface of the sheet. Therefore, the electric field will be uniform and directed away from the sheet on both sides.
Φ=∫E⋅dA
Since the electric field is uniform and perpendicular to the area vector on the flat surfaces, we can write:
Φ=E⋅Atop+E⋅Abottom+0=E⋅A+E⋅A=2EA
where A is the area of one of the flat surfaces of the cylinder.
According to Gauss's law:
Φ=Qencϵ0
where Qenc is the charge enclosed by the Gaussian surface. The charge on the sheet that contributes to the electric field is:
Qenc=σA
Thus, we can write:
2EA=σAϵ0
Now, we can cancel A from both sides (assuming A≠0):
2E=σϵ0
Therefore, the electric field E is:
E=σ2ϵ0
The electric field due to an infinite non-conducting sheet of surface charge density σ at a distance r from it is:
E=σ2ϵ0
Similar Questions
Electric field due to disc and infinite charged layer
View SolutionIn front of a uniformly charged infinite non-conducting sheet of surface charge density σ, a point charge q0 is shifted slowly from a distance a to b(b>a). If work done by external agent is W, then find out relation between the given parameters.
View Solution
Knowledge Check
Electric field intensity at a point due to an infinite sheet of charge having surface charge density σ is E.If sheet were conducting electric intensity would be
AE/2BEC2ED4E
Determine and draw the graph of electric field due to infinitely large non-conducting sheet of thickness t and uniform volume charge density ρ as a function of distance x from its symmetry plane.
(a) x<t2 (b) x≥t2
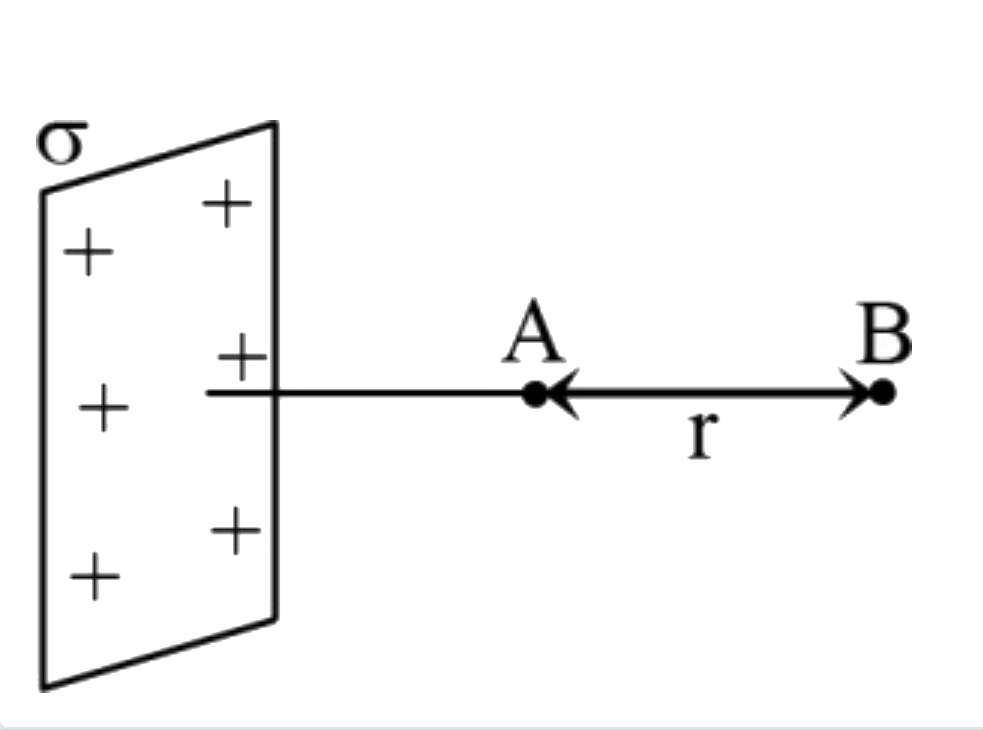
View SolutionAn infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
View SolutionElectric Field Due To An Infinite Line Charge
View Solution(a) Use Gauss's theorem to find the electric field due to a uniformly charged infinitely
Iarge plane thin sheet with surface charge density.Σ
(b) An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the
expression for the amount of work done in bringing a point charge q from infinity to a
point , distant r, in front of the charged plane sheet.
View SolutionWrite the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View SolutionElectric field due to Infinite wire, Ring, Disc, Infinite sheet
View SolutionTwo infinite non-conducting sheets each with uniform surface charge density sigma are kept in such a way that the angle between them is 30^(@). The electric field in the region I shown between them is
View Solution
