Two equal point charges A and B are R distance apart. A third point charge placed on the perpendicular bisector at a disttance d from the centre will experience maximum electrostatic force when
d=R2√2
d=R√2
d=R√2
d=2√2 R
The correct Answer is:A
To solve the problem of determining the distance d at which a third point charge experiences maximum electrostatic force due to two equal point charges A and B separated by a distance R, we can follow these steps:
Step 1: Understand the Configuration
We have two equal point charges Q located at points A and B, separated by a distance R. A third charge Q′ is placed on the perpendicular bisector of the line joining A and B at a distance d from the midpoint O of AB.
Step 2: Calculate the Distance from the Charges to the Third Charge
The distance from each charge A and B to the third charge Q′ can be calculated using the Pythagorean theorem. The distance from O to either charge is R2, and the distance from O to Q′ is d. Thus, the distance r from each charge to the third charge is given by:
r=√d2+(R2)2
Step 3: Calculate the Electrostatic Force on the Third Charge
The electrostatic force F acting on the charge Q′ due to each charge Q is given by Coulomb's law:
F=kQ⋅Q′r2
Substituting r:
F=kQ⋅Q′d2+(R2)2
Step 4: Determine the Net Force
Since both charges exert forces on Q′ in the same direction (along the line connecting A and B), the net force Fnet acting on Q′ is:
Fnet=2Fcos(θ)
where θ is the angle between the line connecting Q and Q′ and the perpendicular bisector. Using trigonometry, we find:
cos(θ)=R2r=R2√d2+(R2)2
Thus, the net force can be expressed as:
Fnet=2⋅kQ⋅Q′d2+(R2)2⋅R2√d2+(R2)2
Step 5: Maximize the Net Force
To find the maximum force, we differentiate Fnet with respect to d and set the derivative equal to zero:
ddd(Fnet)=0
This involves applying the product and chain rules of differentiation.
Step 6: Solve for d
After differentiating and simplifying, we find that the condition for maximum force leads us to:
d2=R28
Thus, taking the square root gives:
d=R2√2
Conclusion
The distance d at which the third charge experiences maximum electrostatic force is:
R2√2
We have two equal point charges Q located at points A and B, separated by a distance R. A third charge Q′ is placed on the perpendicular bisector of the line joining A and B at a distance d from the midpoint O of AB.
The distance from each charge A and B to the third charge Q′ can be calculated using the Pythagorean theorem. The distance from O to either charge is R2, and the distance from O to Q′ is d. Thus, the distance r from each charge to the third charge is given by:
r=√d2+(R2)2
The electrostatic force F acting on the charge Q′ due to each charge Q is given by Coulomb's law:
F=kQ⋅Q′r2
Substituting r:
F=kQ⋅Q′d2+(R2)2
Since both charges exert forces on Q′ in the same direction (along the line connecting A and B), the net force Fnet acting on Q′ is:
Fnet=2Fcos(θ)
where θ is the angle between the line connecting Q and Q′ and the perpendicular bisector. Using trigonometry, we find:
cos(θ)=R2r=R2√d2+(R2)2
Thus, the net force can be expressed as:
Fnet=2⋅kQ⋅Q′d2+(R2)2⋅R2√d2+(R2)2
To find the maximum force, we differentiate Fnet with respect to d and set the derivative equal to zero:
ddd(Fnet)=0
This involves applying the product and chain rules of differentiation.
After differentiating and simplifying, we find that the condition for maximum force leads us to:
d2=R28
Thus, taking the square root gives:
d=R2√2
The distance d at which the third charge experiences maximum electrostatic force is:
R2√2
Similar Questions
Two particles A and B having equal charges are placed at distance d apart. A third charged particle placed on the perpendicular bisector at a distance x will experience the maximum Coulomb’s force when :
View SolutionInside a neutral hollow conducting sphere of radius X and centre C, a point charge q is placed as shown in the figure. Another point charge q1, is placed outside the sphere at distance d from centre. The net- electrostatic force on charge q placed at the centre is K=14πε0

View Solution
Knowledge Check
Two equal charges are separated by a distance d. A third charge placed on a perpendicular bisector at x distance will experience maximum coulomb force when
Ax=d√2Bx=d2Cx=d2√2Dx=d2√3Two point charges +q and −q are placed a distance x apart. A third charge is so placed that al the three charges are in equilibrium. Then
Auknknown charge is −4q/9Bunknown charge is −9q/4Cit should be at (x/3)from smaller chargge between themDnone of theseA charge Q is kept at the centre of a conducting sphere of inner radius R1 and outer radius R2. A point charge q is kept at a distance r(>R2) from the centre. If q experiences an electrostatic force 10 N then assuming that no other charges are present, electrostatic force experienced by Q will be :
A−10NB0C20NDnone of these
Two free charges q and 4q are placed at a distance d apart A third charge Q is placed between them at a distance x from charge q such that the system is in equilibrium. Then
View SolutionTwo free charges q and 4q are placed at a distance d apart A third charge Q is placed between them at a distance x from charge q such that the system is in equilibrium. Then magnitude of third charge and postion,
View SolutionTwo point metal charges−q and +2q are placed at a certain distance apart.Where should a third point charge be placed so that it is in equilibrium?
View SolutionThe force of repulsion between two point charges is F, when they are d distance apart. If the point charges are replaced by conducted sphereas each of radius r and the charges remain same. The separation between the centre of sphere isd, then force of repulsion between them is
View SolutionTwo identical bar magnets are fixed with their centres at a distance d apart. A stationary charge Q is placed at P in between the gap of the two magnets at distance D from the centre O as shown in the figure. The force on the charge Q is
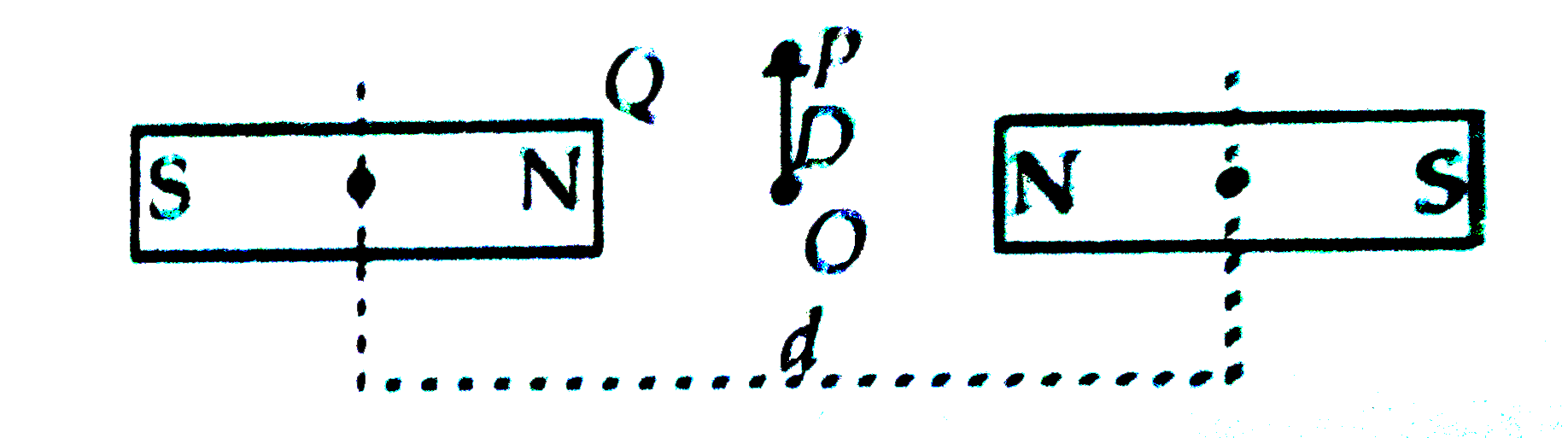
View Solution
