A charge q is to be distributed on two conducting spheres. What should be the value of the charges on the spheres so that the repulsive force between them is maximum when they are placed at a fixed distance from each other in air ?
q2 and q2
q4 and 3q4
q3 and 2q3
q5 and 4q5
The correct Answer is:A
To solve the problem of distributing a charge q on two conducting spheres such that the repulsive force between them is maximized, we can follow these steps:
Step 1: Define the Charges on the Spheres
Let the charge on the first sphere be x and the charge on the second sphere be q−x. Since the spheres are conducting, the charge will distribute uniformly on each sphere.
Step 2: Write the Expression for the Force
According to Coulomb's law, the force F between two point charges is given by:
F=k|x⋅(q−x)|d2
where k is Coulomb's constant, and d is the distance between the centers of the spheres.
Step 3: Simplify the Force Equation
We can express the force as:
F=kd2(x(q−x))=kd2(qx−x2)
Step 4: Differentiate the Force with Respect to x
To find the value of x that maximizes the force, we differentiate F with respect to x:
dFdx=kd2(q−2x)
Step 5: Set the Derivative to Zero
To find the maximum force, we set the derivative equal to zero:
q−2x=0
Solving for x, we get:
2x=q⟹x=q2
Step 6: Determine the Charges on Each Sphere
Since x=q2, the charge on the first sphere is q2 and the charge on the second sphere is:
q−x=q−q2=q2
Conclusion
Thus, the charges on the two spheres should be:
- Charge on Sphere 1: q2
- Charge on Sphere 2: q2
This distribution maximizes the repulsive force between the two spheres when they are placed at a fixed distance from each other in air.
Let the charge on the first sphere be x and the charge on the second sphere be q−x. Since the spheres are conducting, the charge will distribute uniformly on each sphere.
According to Coulomb's law, the force F between two point charges is given by:
F=k|x⋅(q−x)|d2
where k is Coulomb's constant, and d is the distance between the centers of the spheres.
We can express the force as:
F=kd2(x(q−x))=kd2(qx−x2)
To find the value of x that maximizes the force, we differentiate F with respect to x:
dFdx=kd2(q−2x)
To find the maximum force, we set the derivative equal to zero:
q−2x=0
Solving for x, we get:
2x=q⟹x=q2
Since x=q2, the charge on the first sphere is q2 and the charge on the second sphere is:
q−x=q−q2=q2
Thus, the charges on the two spheres should be:
- Charge on Sphere 1: q2
- Charge on Sphere 2: q2
Similar Questions
A charge Q is to be divided on two objects. What shouold. be the values of the charges on the objects so that the. force between the objects can be maximum?.
View Solution(a) Two protons are placed at some separation in vacuum. Find the ratio of electric and gravitational force acting between them.
(b) Two point charges are placed at separation 3m in vacuum. What can be the minimum force between them.
(c ) A charge Q is to be divided on two objects. What should be the value of the charges in the objects so that the force between them is maximum ?
(d) Two insulating small spheres are rubbed against each other and placed 1.6cm apart. If they attract each other with a force of 0.9N, how many electrons were transferred from one sphere to the other during rubbing ?
View Solution
Knowledge Check
A charge Q is divided into two parts. Charge on each part is q. Also, Q/q=2. What is the Columbic force between two charges q and q when both parts are placed certain distance apart?
AForce is equal in magnitude for both but opposite in directionBForce is dependent on the medium in which charges are placedCForce is maximum irrespective of medium in which charges are placedDNone of the aboveParagraph for Questions 53 and 54: An isolated system consists of two conducting spheres A and B. Sphere A has five times the radius of sphere B. Initially, the spheres are given equal amounts of positive charge and are isolated from each other. The two spheres are then connected by a conducting wire.
Note: The potential of a sphere of radius R that carries a charge Q is V=kQ/R, if the potential at infinity is zero.
Determine the ratio of the charge on sphere A to that on sphere B,qA/qB, after the spheres are connected by the wire.A1B1/5C5D25There is a cubical cavity inside a conducting sphere of radius R. A positive point charge Q is placed at the centre of the cube and another positive charge q is placed at a distance 1(>R) from the centre of the sphere. The sphere is earthed
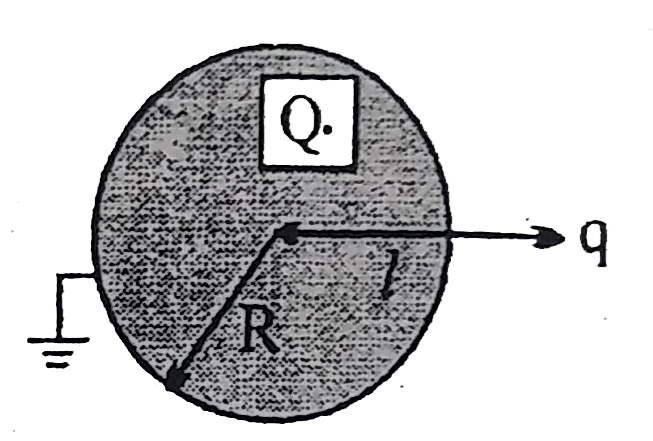
Net charge on the outer surface of conducting sphere isA+QBQ−qR/1C−qR/IDnone
A charge is divided into two charges q and (Q-q) .The value of q so that force between them is maximum is equal to
View SolutionAt what distance should two charges, each equalk to 1C, be placed so that the force between them equals your weight?
View SolutionTotal charge Q is divided between two point objects in such a manner that electric force of repulsion between them is maximum when placed at a separation d from each other. What is the magnitude of this maximum possible electrostatic force between them?
View SolutionHow is force between two charges affected when each charge is doubled and distance between them is also doubled?
View SolutionTwo point charges repel each other with a force F when placed in water of dielectric constant 81. What will be the force between them when placed the same distance apart in air ?
View Solution
