A charged body has an electric flux F assoclated with it. Now if the body is placed inside a conducting shell tthen the electric flux outside the shell is
Zero
Greater then F
Less then F
Equal to F
The correct Answer is:D
To solve the question regarding the electric flux outside a conducting shell when a charged body is placed inside it, we can follow these steps:
1. Understanding Electric Flux:
Electric flux (Φ) through a surface is defined by the equation:
Φ=Qinε0
where Qin is the charge enclosed by the surface and ε0 is the permittivity of free space.
2. Given Information:
We are given that a charged body has an electric flux F associated with it. This implies:
F=Qε0
where Q is the charge of the body.
3. Placing the Charged Body Inside a Conducting Shell:
When the charged body is placed inside a conducting shell, the electric field inside the conductor must be zero. According to Gauss's law, if the electric field E is zero, then:
Φ=E⋅A=0
This means that the net charge inside the conducting shell must also be zero.
4. Induction of Charges:
The charge Q on the charged body will induce a charge of −Q on the inner surface of the conducting shell. Consequently, a charge of +Q will appear on the outer surface of the conducting shell to maintain the neutrality of the shell.
5. Calculating the Electric Flux Outside the Shell:
To find the electric flux outside the conducting shell, we can consider a Gaussian surface that encloses the entire shell. The total charge enclosed by this Gaussian surface is +Q (the charge on the outer surface of the shell). Therefore, the electric flux through this Gaussian surface is given by:
Φoutside=Qouterε0=Qε0
6. Relating Back to Given Flux:
Since we established that F=Qε0, we can conclude that:
Φoutside=F
Final Answer:
The electric flux outside the conducting shell is F.
---
Electric flux (Φ) through a surface is defined by the equation:
Φ=Qinε0
where Qin is the charge enclosed by the surface and ε0 is the permittivity of free space.
We are given that a charged body has an electric flux F associated with it. This implies:
F=Qε0
where Q is the charge of the body.
When the charged body is placed inside a conducting shell, the electric field inside the conductor must be zero. According to Gauss's law, if the electric field E is zero, then:
Φ=E⋅A=0
This means that the net charge inside the conducting shell must also be zero.
The charge Q on the charged body will induce a charge of −Q on the inner surface of the conducting shell. Consequently, a charge of +Q will appear on the outer surface of the conducting shell to maintain the neutrality of the shell.
To find the electric flux outside the conducting shell, we can consider a Gaussian surface that encloses the entire shell. The total charge enclosed by this Gaussian surface is +Q (the charge on the outer surface of the shell). Therefore, the electric flux through this Gaussian surface is given by:
Φoutside=Qouterε0=Qε0
Since we established that F=Qε0, we can conclude that:
Φoutside=F
The electric flux outside the conducting shell is F.
Similar Questions
If a hemispherical body is placed in a uniform electric field E then the flux linked with the curved surface is E B
View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
View Solution
Knowledge Check
A charged body has an electric flux ϕ associated with it. The body is now placed inside a metallic container. The flux ϕ, outside the container will be
AZeroBEqual to ϕCGreater than ϕDLess than ϕA charged body has an electric flux ϕ associated with it. The body is now placed inside a metallic container. The flux ϕ, outside the container will be
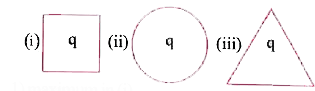
AZeroBEqual to ϕCGreater than ϕDLess than ϕA charge q is enclosed as shown below the electric flux is
 Amaximum inBmaximum inCmaximum inDequal in all
Amaximum inBmaximum inCmaximum inDequal in all
A positive point charge is placed inside a spherical metallic shell. The electric field lines are represented by
View SolutionA charge q is enclosed as shown, below the electric flux is
View SolutionFine electric dipoles of charge 'q' each are placed into the shell .What will be the amount of electric flux associated with shell ?
View SolutionEight dipoles of charges of magnitude e are placed inside a cube. The total electric flux coming out of the cube will be
View SolutionTen dipoles ,each of dipole moment 'p' , are placed inside a hollow sphere . The total electric flux coming out of the sphere will be
View Solution
