The dimensional formula of linear charge density λ is
[M−1L−1T+1A]
[M0L−1T+1A]
[M−1L−1T+1A−1]
[M0L−1T+1A−1]
The correct Answer is:B
To find the dimensional formula of linear charge density (λ), we need to understand what linear charge density represents. Linear charge density is defined as the charge per unit length.
1. Define Linear Charge Density:
λ=QL
where Q is the charge and L is the length.
2. Find the Dimensional Formula of Charge (Q):
Charge Q can be expressed in terms of current I and time t:
Q=I⋅t
The dimensional formula for current I is (I)=A (Ampere), and for time t it is (t)=T. Therefore, the dimensional formula for charge Q becomes:
(Q)=(I)(t)=A⋅T
3. Find the Dimensional Formula of Length (L):
The dimensional formula for length L is:
(L)=L
4. Substitute into the Formula for λ:
Now, substituting the dimensional formulas for Q and L into the equation for λ:
(λ)=(Q)(L)=A⋅TL
5. Express the Dimensional Formula:
This can be expressed as:
(λ)=A⋅T⋅L−1
or in a more standard form:
(λ)=M0⋅L−1⋅T1⋅A1
Final Answer:
The dimensional formula of linear charge density λ is:
M0L−1T1A1
λ=QL
where Q is the charge and L is the length.
Charge Q can be expressed in terms of current I and time t:
Q=I⋅t
The dimensional formula for current I is (I)=A (Ampere), and for time t it is (t)=T. Therefore, the dimensional formula for charge Q becomes:
(Q)=(I)(t)=A⋅T
The dimensional formula for length L is:
(L)=L
Now, substituting the dimensional formulas for Q and L into the equation for λ:
(λ)=(Q)(L)=A⋅TL
This can be expressed as:
(λ)=A⋅T⋅L−1
or in a more standard form:
(λ)=M0⋅L−1⋅T1⋅A1
The dimensional formula of linear charge density λ is:
M0L−1T1A1
Similar Questions
Knowledge Check
- Question 1 - Select One
The dimensional formula of relative density is
AML−3BLT−1CMLT−2DDimensionaless - Question 2 - Select One
The dimensional formula of relative density is
AML−3BLT−1CMLT−2DDimensionless - Question 3 - Select One
The dimensional formula of magnetic flux density is :
AM1L2T1I−1BM1T−2I−1CM1L2T−2I−1DM1L1T−2I−1
The dimensional formula for strain energy density is
View SolutionAn infinitely long line of linear charge density λ is shown in the figure. The potential difference VA−VB between the two points A and B is
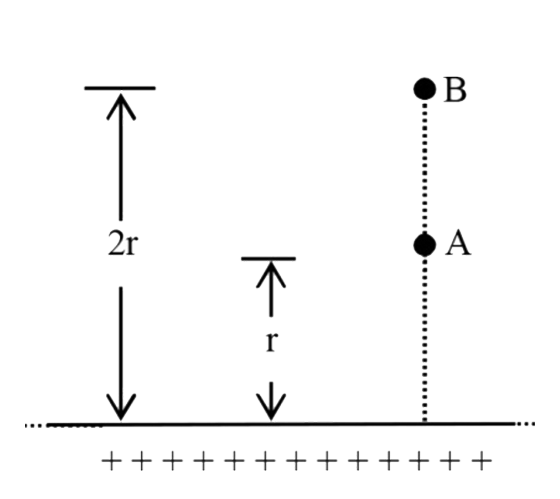 View Solution
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
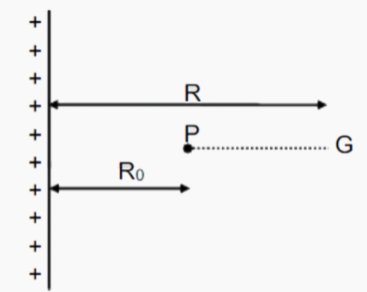 View Solution
View SolutionThe dimensional formula of linear momentum of a system is:
View SolutionTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -
 View Solution
View Solution

