The armature of a generator of resistance 1Ω is rotated at its rated speed and produces 125 V without load and 115 V with full load. The current in the armature coil is
240 A
10 A
1 A
2A
The correct Answer is:B
To find the current in the armature coil of the generator, we can follow these steps:
1. Identify the Given Values:
- Resistance of the armature (R) = 1 Ω
- Voltage without load (E) = 125 V
- Voltage with full load (V) = 115 V
2. Understand the Concept of Back EMF:
- When the generator is under full load, the voltage across the armature is less than the no-load voltage due to the back EMF (E_b) generated. The back EMF opposes the applied voltage.
3. Calculate the Back EMF:
- The back EMF can be calculated as:
Eb=E−V
- Substituting the values:
Eb=125V−115V=10V
4. Apply Ohm's Law to Find the Current:
- The current (I) in the armature can be calculated using Ohm’s Law:
I=VR
- Here, V is the voltage across the armature when it is under load, which is 115 V, and R is the resistance of the armature:
I=115V1Ω=115A
5. Calculate the Current Considering Back EMF:
- The effective voltage that drives the current through the armature is the difference between the voltage with no load and the back EMF:
I=EbR=10V1Ω=10A
6. Final Answer:
- The current in the armature coil is 10 A.
- Resistance of the armature (R) = 1 Ω
- Voltage without load (E) = 125 V
- Voltage with full load (V) = 115 V
- When the generator is under full load, the voltage across the armature is less than the no-load voltage due to the back EMF (E_b) generated. The back EMF opposes the applied voltage.
- The back EMF can be calculated as:
Eb=E−V
- Substituting the values:
Eb=125V−115V=10V
- The current (I) in the armature can be calculated using Ohm’s Law:
I=VR
- Here, V is the voltage across the armature when it is under load, which is 115 V, and R is the resistance of the armature:
I=115V1Ω=115A
- The effective voltage that drives the current through the armature is the difference between the voltage with no load and the back EMF:
I=EbR=10V1Ω=10A
- The current in the armature coil is 10 A.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -C) Previous Years Questions23videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)15videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - A) (OBJECTIVE TYPE QUESTIONS)30videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH INSTITUTECHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION -J(Aakash Challengers Questions)5videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions25videos
ELECTROMAGNETIC WAVES
Similar Questions
A motor having an armature of resistance 2.0Ω operates on 220 V mains. At full speed, it develops a back emf of 210 V. Find the current in the armature just when the motor is switched on (assuming that no starter is used) and when running at full speed. Also fined the efficiency of the motor at full speed.
View SolutionA motor having an armature of resistance 2.0 ohm operates on 220 V mains. At its full speed, it develops a back e.m.f. of 210 V. Find the currents in the armature when motor is switched on and when running at full speed. What is the efficiency ot the motor at full speed ?
View Solution
Knowledge Check
- Question 1 - Select One
A 1250 W heater operates at 115V. What is the resistance of the heating coil?
A1.6ΩB13.5ΩC1250ΩD10.6Ω - Question 2 - Select One
4 cells each of emf 2 V and internal resistance of 1Ω are connected in parallel to a load resistor of 2Ω. Then the current through the load resistor is
A2AB1.5AC1AD0.888A - Question 3 - Select One
A motor having an armature of resistance 2Ω is designed to operate at 220V mains. At full speed, it devlops a back e.m.f. of 210V. When the motor is running at full speed, the current in the armature is
A5AB105AC110AD215A
A 5 V battery with internal resistance 2Ω and a 2V battery with internal resistance 1Ω are connected to a 10Ω as shown in the figure.
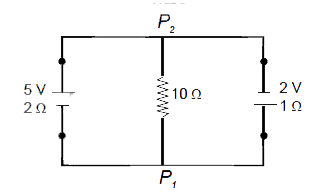
The current in the 10Ω resistance isView SolutionA motor runs at 20 V. The resistance of the armature is 11 ohm. If the back emf produced is 198 V, when at full speed, then calculate the current through armature, when (i) motor is just switched on and (ii) motor is at full speed.
View SolutionA heating coil has a resistance of 200Ω. At what rate will heat be produced in it when a current of 2.5A flows through it?
View SolutionThe armature of a dc motor has 20Ω resistance It draws a currrent of 1.5 A when run by a 220V dc supply The value of the block emf induced in it is .
View SolutionThe balancing length on a potentiometer wire with a cell of emf 2V and internal resistance 1Ω connected in the secondary circuit with no load is 200cm. If a resistor of 19Ω is connected parallel to the cell, the balancing length
View Solution

