The minimum deviation produced by a glass prism of angle 40∘ is 36∘. The refractive index of the glass will be
1.4
1.2
1.5
1.8
The correct Answer is:D
To find the refractive index of the glass prism given the angle of the prism and the minimum deviation, we can use the formula for the refractive index (μ) of a prism:
μ=sin(A+Dm2)sin(A2)
Where:
- A is the angle of the prism,
- Dm is the minimum deviation.
1. Identify the given values:
- Angle of the prism, A=40∘
- Minimum deviation, Dm=36∘
2. Calculate A+Dm2:
A+Dm=40∘+36∘=76∘
A+Dm2=76∘2=38∘
3. Calculate A2:
A2=40∘2=20∘
4. Substitute these values into the refractive index formula:
μ=sin(38∘)sin(20∘)
5. Calculate sin(38∘) and sin(20∘):
- Using a calculator:
- sin(38∘)≈0.6157
- sin(20∘)≈0.3420
6. Calculate the refractive index μ:
μ=0.61570.3420≈1.80
Final Answer:
The refractive index of the glass is approximately μ≈1.80.
- A is the angle of the prism,
- Dm is the minimum deviation.
- Angle of the prism, A=40∘
- Minimum deviation, Dm=36∘
A+Dm=40∘+36∘=76∘
A+Dm2=76∘2=38∘
A2=40∘2=20∘
μ=sin(38∘)sin(20∘)
- Using a calculator:
- sin(38∘)≈0.6157
- sin(20∘)≈0.3420
μ=0.61570.3420≈1.80
The refractive index of the glass is approximately μ≈1.80.
Similar Questions
The angle of minimum deviation produced by a 60∘ prism is 40∘. Calculate the refractive index of the material of the prism.
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be 40∘. What is the refractive index of the materal of the prism? The refracting angle of the prism is 60∘. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of parallel beam of light.
View Solution
Knowledge Check
- Question 1 - Select One
The refractive index of glass is minimum for
Ared lightBgreen lightCyellow lightDviolet light - Question 2 - Select One
The angle of minimum deviation produced by an equilateral prism is 46∘ The refractive index of material of the prism.
A1.6B1.5C1.4D1.8 - Question 3 - Select One
The angle of minimum deviation measured with a prism is 30∘ and the angle of prism is 60∘ . The refractive index of the prism material is
A√2B2C32D43
A prism is made of glass of unknown refractive index.A parallel beam of light is incidence on the first refracting face of prism.The angle of minimum deviation is measured to be 40∘ .What is the refractive index of material of the prism? The refracting angle of prism is 60∘. [sin50∘=0.766]]
View SolutionFor a glass prism the plot of deviation (δ) vs angle of incidence (i) is as shown. Find the refractive index of the glass and value of angle i1.
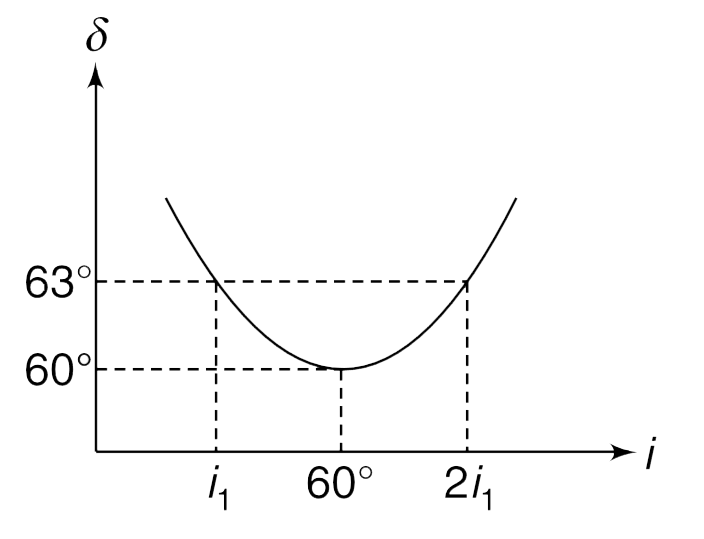 View Solution
View SolutionThe least angle of deviation for a glass prism is equal to its refracting angle. The refractive index of glass is 1.5. Then the angle of the prism is
View SolutionThe angle of incidence for a ray of light at a refracting surface of a prism is 45∘. The angle of prism is 60∘ . If the ray suffers minimum deviation through the prism. The angle of minimum deviation and refractive index of the material of the prism respectively, are
View SolutionThe angle of incidence for a ray of light at a refracting surface of a prism is 45∘. The angle of prism is 60∘. If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are :
View Solution

