The energies of three consecutive energy levels L3,L2andL1 of hydrogen atom are E0,4E09 and E04 respectively. A photon of wavelength λ is emitted for a transition L3→L1 . What will be the wavelength of emission for transition L2→L1?
16λ31
27λ7
1920λ
`lambda`
The correct Answer is:B
To solve the problem, we need to find the wavelength of emission for the transition from energy level L2 to L1 in a hydrogen atom, given the energies of the three consecutive energy levels L3, L2, and L1.
1. Identify the Energy Levels:
- Given:
- EL3=E0
- EL2=4E09
- EL1=E04
2. Calculate the Energy Change for Transition L3→L1:
- The energy change (ΔE31) for the transition from L3 to L1 is:
ΔE31=EL3−EL1=E0−E04=3E04
3. Relate Energy Change to Wavelength:
- According to Planck's law, the energy of a photon is given by:
E=hcλ
- Setting the energy change equal to the energy of the emitted photon:
3E04=hcλ
- Rearranging gives us:
λ=hc3E04=4hc3E0
4. Calculate the Energy Change for Transition L2→L1:
- The energy change (ΔE21) for the transition from L2 to L1 is:
ΔE21=EL2−EL1=4E09−E04
- To subtract these fractions, we need a common denominator. The least common multiple of 9 and 4 is 36:
ΔE21=(4E09⋅44)−(E04⋅99)=16E036−9E036=7E036
5. Relate Energy Change to Wavelength for Transition L2→L1:
- Using Planck's law again:
ΔE21=hcλ1
- Setting the energy change equal to the energy of the emitted photon gives:
7E036=hcλ1
- Rearranging gives us:
λ1=hc7E036=36hc7E0
6. Relate the Two Wavelengths:
- From the previous steps, we have:
λ=4hc3E0
- Now, we can express λ1 in terms of λ:
λ1=36hc7E0=367⋅hcE0=367⋅43λ=487λ
Final Answer:
The wavelength of emission for the transition L2→L1 is:
λ1=487λ
- Given:
- EL3=E0
- EL2=4E09
- EL1=E04
- The energy change (ΔE31) for the transition from L3 to L1 is:
ΔE31=EL3−EL1=E0−E04=3E04
- According to Planck's law, the energy of a photon is given by:
E=hcλ
- Setting the energy change equal to the energy of the emitted photon:
3E04=hcλ
- Rearranging gives us:
λ=hc3E04=4hc3E0
- The energy change (ΔE21) for the transition from L2 to L1 is:
ΔE21=EL2−EL1=4E09−E04
- To subtract these fractions, we need a common denominator. The least common multiple of 9 and 4 is 36:
ΔE21=(4E09⋅44)−(E04⋅99)=16E036−9E036=7E036
- Using Planck's law again:
ΔE21=hcλ1
- Setting the energy change equal to the energy of the emitted photon gives:
7E036=hcλ1
- Rearranging gives us:
λ1=hc7E036=36hc7E0
- From the previous steps, we have:
λ=4hc3E0
- Now, we can express λ1 in terms of λ:
λ1=36hc7E0=367⋅hcE0=367⋅43λ=487λ
The wavelength of emission for the transition L2→L1 is:
λ1=487λ
Similar Questions
Knowledge Check
The energies of three conservative energy levels L3,L2 and L1 of hydrogen atom are E0. 4E09 and E04 respectively. A photon of wavelength λ is emitted for a transition L3 to L1 .What will be the wavelength of emission for transition L2 to L1 ?
A16λ31B27λ7C1920λDλThe energy of a I,II and III energy levels of a certain atom are E,4E3 and 2E respectively. A photon of wavelength λ is emitted during a transition from III to I. what will be the wavelength of emission for II to I?
Aλ2BλC2λD3λThree energy levels L1,L2 and L3 of a hydrogen atom correspond to increasing values of energy i.e., EL1<EL2<EL3 . If the wavelength corresponding to the transitions L3 to L2,L2 to L1 and L3 to L1 are λ3,λ2 and λ1 respectively then
Aλ3=λ1+λ2Bλ1=λ2λ3λ2+λ3Cλ1=λ2+λ3Dλ3=λ1λ2λ1+λ2
Two bodies with moment of inertia l1 and l2 (l1>l2) have equal angular momentum. If E1 and E2 are the rotational kinetic energies, then
View SolutionA Hydrogen atom and Li++ ion are both in the second excited state. If LH and LLi are their respective angular momenta, and EH and ELi their respective energies, then:
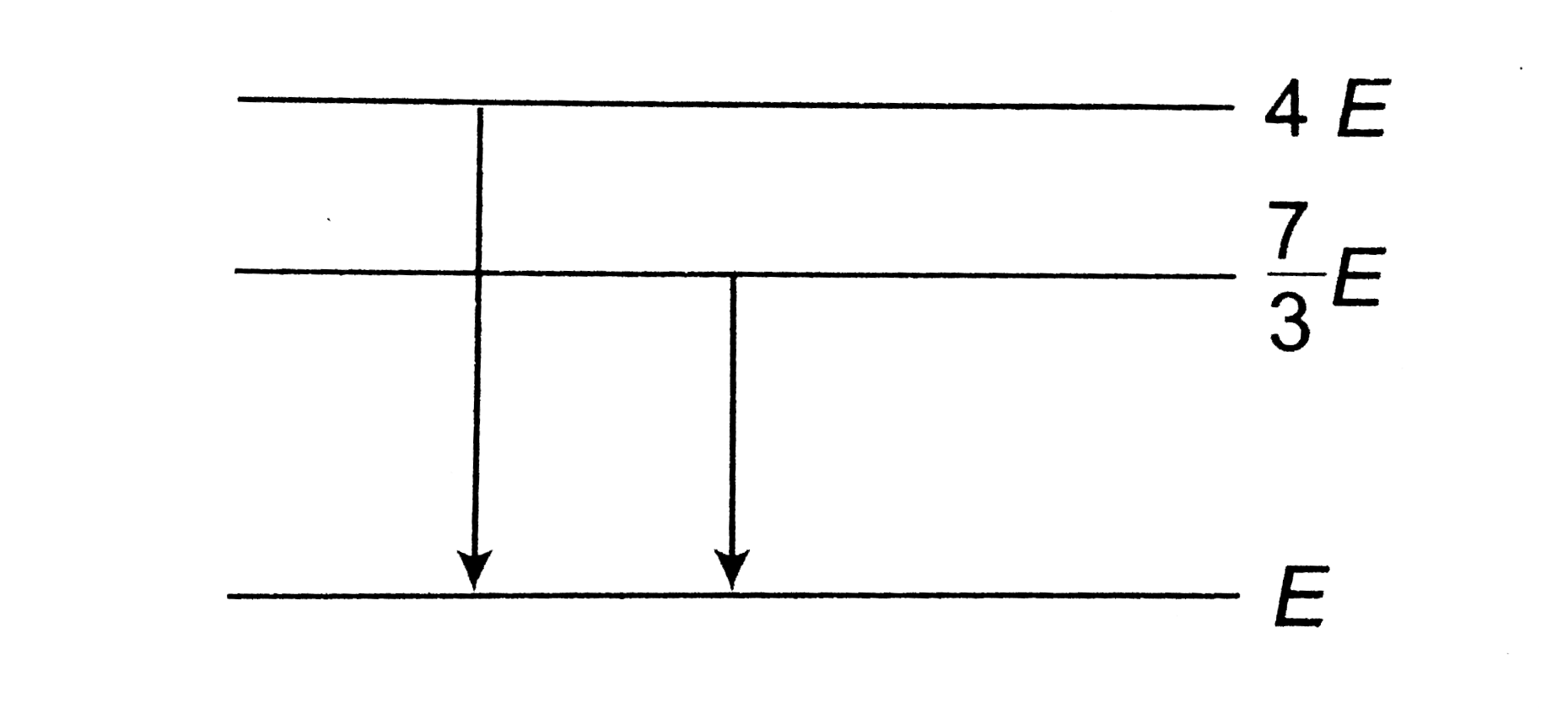
View SolutionThe following diagram indicates the energy levels of a certain atom when the system moves from 4E level to E. A photon of wavelength λ1 is emitted. The wavelength of photon produced during its transition from 73E level to E is λ2. the ratio λ1λ2 will be
View SolutionThe balancing lengths for the cells of e.m.f. E1 and E2 are l1 and l2 respectively. If they are connected separately then
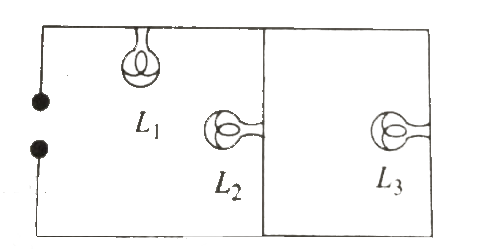
View SolutionFigure 7.44 shows three similar lamps L1,L2,andL3 connectged across a power supply. If the lamp L3 fuses, how will the light emitted by L1andL2 change?
View Solution
