The rate of a reaction increases by 2.5 times when the temperature is raised from 300K to 310K. If K is the rate constant at 310 K will be equal to
K
2K
2.5K
3K
The correct Answer is:C
To solve the problem, we need to use the Arrhenius equation and the concept of the temperature coefficient. The Arrhenius equation relates the rate constant (k) to temperature (T) as follows:
k=Ae−EaRT
Where:
- k = rate constant
- A = pre-exponential factor
- Ea = activation energy
- R = universal gas constant (8.314 J/(mol·K))
- T = temperature in Kelvin
Given that the rate of the reaction increases by 2.5 times when the temperature is raised from 300 K to 310 K, we can express this relationship as:
k2k1=2.5
Where:
- k1 = rate constant at 300 K
- k2 = rate constant at 310 K
Using the Arrhenius equation, we can write:
k2k1=Ae−EaR⋅310Ae−EaR⋅300
This simplifies to:
k2k1=e−EaR⋅310+EaR⋅300
This can be further simplified to:
k2k1=eEaR(1300−1310)
Now, we can calculate 1300−1310:
1300−1310=310−300300×310=1093000=19300
Substituting this back into the equation gives:
k2k1=eEaR⋅9300
Now, we know that k2k1=2.5, so we can write:
2.5=eEaR⋅9300
Taking the natural logarithm on both sides:
ln(2.5)=EaR⋅9300
Now, we can express k2 in terms of k1:
k2=k1⋅2.5
If we assume k1 is the rate constant at 300 K, we can use this relationship to find k2 once we know k1.
However, since we are not given k1, we can conclude that k2 is 2.5 times k1.
Final Answer:
If k1 is the rate constant at 300 K, then k2=2.5⋅k1.
- k = rate constant
- A = pre-exponential factor
- Ea = activation energy
- R = universal gas constant (8.314 J/(mol·K))
- T = temperature in Kelvin
- k1 = rate constant at 300 K
- k2 = rate constant at 310 K
If k1 is the rate constant at 300 K, then k2=2.5⋅k1.
Topper's Solved these Questions
- CHEMICAL KINETICSBook:AAKASH INSTITUTEChapter:CHEMICAL KINETICSExercise:ASSIGNMENT (SECTION B : Objective Type Questions)
Explore 20 Videos
- CHEMICAL KINETICSBook:AAKASH INSTITUTEChapter:CHEMICAL KINETICSExercise:ASSIGNMENT (SECTION C : Previous Year Questions)
Explore 62 Videos
- CHEMICAL KINETICSBook:AAKASH INSTITUTEChapter:CHEMICAL KINETICSExercise:EXERCISE
Explore 30 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTURE Book:AAKASH INSTITUTEChapter:CHEMICAL BONDING AND MOLECULAR STRUCTURE Exercise:Assignment Section J (Aakash Challengers Questions)
Explore 10 Videos
- CHEMISTRY IN EVERYDAY LIFE Book:AAKASH INSTITUTEChapter:CHEMISTRY IN EVERYDAY LIFE Exercise:Assignment ( SECTION - A)
Explore 45 Videos
Similar Questions
The rate of a reaction increases to 2.3 times when the temperature is raised form 300K to 310K. If Q is the rate constant at 300K, then the rate constant at 310K will be equal to
View SolutionThe rate of a reaction increases to four times when the prevailing temperature is raised from 300 K to 320 K. Calculate the energy of activation of this reaction assuming that it does not change with temperature. [R=8.314J mol−1K−1]
View Solution
Knowledge Check
The rate of a certain reaction increases by 2.5 times when the temperature is raised from 300K at 310K. If k is the rate constant at 300K then the rate constant at 310 K will be equal to
AkB2kC2.5kD3kThe rate of a certain reaction increases by 2.3 times when the temperature is raised form 300K to 310K. If k is the rate constant at 300K, then the rate constant at 310K will be equal to
A2kBkC2.3kD3k2When the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes K as a function of temperature, i.e.
k=Ae−Ea/RT
where
k= rate constant
A= a constant (frequency factor)
Ea= energy of activation
log10k=log10A−Ea2.303R[1R]
Y=C+MX
It is the equation of straight line with negative slope. On plotting log10k against [1T] we get a straight line as shown below :
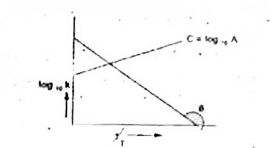
The slope gives activation energy and intercept gives frequency factor.
Also log.k2k1=Ea2.303[T2−T1T1T2]
The rate of certain reaction increases by 2.5 times when the temperature is raised from 300K to 310K. If k is the rate constant at 300K then rate constant at 310K will be equal toAkB2kC2.5kD13k
Two reactions, (i)A→ products and (ii)B→ products , follow first order kinetics. The rate of the reaction (i) is doubled when the temperature is raised from 300K to 310K. The half life for this reaction at 310K is 30 minutes. At the same temperature B decomposes twice as fast as A. If the energy of activation for the reaction (i) is half that of reaction (ii) calculate the rate constant of the reaction (ii) at 300K.
View SolutionThe rate constant of a reaction increases by 7% when its temperature is raised from 300 K to 310 K, while its equilibrium constant increases by 3%. Calculate the activation energy of the forward and reverse reactions.
View SolutionTwo reaction, (I)A→ Products and (II)B→ Products, follow first order kinetics. The rate of reaction (I) is doubled when the temperature is raised form 300K to 310K. The half life for this reaction at 310K is 30min. At the same temperature B decomposes twice as fast as A. If the energy of activation for reaction (II) is twice that of reaction (I), (a) calculate the rate of constant of reaction (II) at 300K.
View SolutionTwo reactions (i)A→P(ii)B→P follow first-order kinetics. The rate of the reaction (i) is doubled when the temperature is raised from 300 K to 310 K. The half-life for this reaction at 310 K is 30 minutes. At the same temperature B decomposes twice as fast as A. If the energy of activation for the reaction (ii) is half that of reaction (i), calculate the rate constant of the reaction (ii) at 300 K.
View SolutionThe activation energy for a reaction when the temperature is raised from 300K to 310K is
View Solution
