An alternating current of rms value 10 A is passed through a resistor. The maximum potential difference across the resistor is:
20V
90V
169.68V
None of these
The correct Answer is:C
To find the maximum potential difference across a resistor when an alternating current (AC) is passed through it, we can follow these steps:
Step 1: Understand the relationship between RMS current and maximum current
The root mean square (RMS) value of current (I_RMS) is related to the maximum current (I_0) by the formula:
I0=√2×IRMS
Step 2: Substitute the given RMS value
Given that the RMS value of the current is 10 A, we can substitute this value into the formula:
I0=√2×10A
Step 3: Calculate the maximum current
Calculating this gives:
I0=√2×10≈1.414×10≈14.14A
Step 4: Use Ohm's law to find the maximum potential difference
The maximum potential difference (V_0) across the resistor can be calculated using Ohm's law:
V0=I0×R
where R is the resistance of the resistor.
Step 5: Substitute the resistance value
Given that the resistance R is 12 Ω, we substitute this value into the equation:
V0=14.14A×12Ω
Step 6: Calculate the maximum potential difference
Calculating this gives:
V0=14.14×12≈169.68V
Final Answer
Thus, the maximum potential difference across the resistor is approximately 169.68 V.
---
The root mean square (RMS) value of current (I_RMS) is related to the maximum current (I_0) by the formula:
I0=√2×IRMS
Given that the RMS value of the current is 10 A, we can substitute this value into the formula:
I0=√2×10A
Calculating this gives:
I0=√2×10≈1.414×10≈14.14A
The maximum potential difference (V_0) across the resistor can be calculated using Ohm's law:
V0=I0×R
where R is the resistance of the resistor.
Given that the resistance R is 12 Ω, we substitute this value into the equation:
V0=14.14A×12Ω
Calculating this gives:
V0=14.14×12≈169.68V
Thus, the maximum potential difference across the resistor is approximately 169.68 V.
Similar Questions
Knowledge Check
- Question 1 - Select One
An alternating current of rms value 10 A is passed through a 12Ω resistor. The maximum potential difference across the resistor is
A20 VB90 VC169.68 VDnone of these - Question 2 - Select One
An alternating current of rms value 10 A is passed through a 12Ω resistor. The maximum potential difference across the resistor is
A20 VB90 VC169.68 VDNone of these - Question 3 - Select One
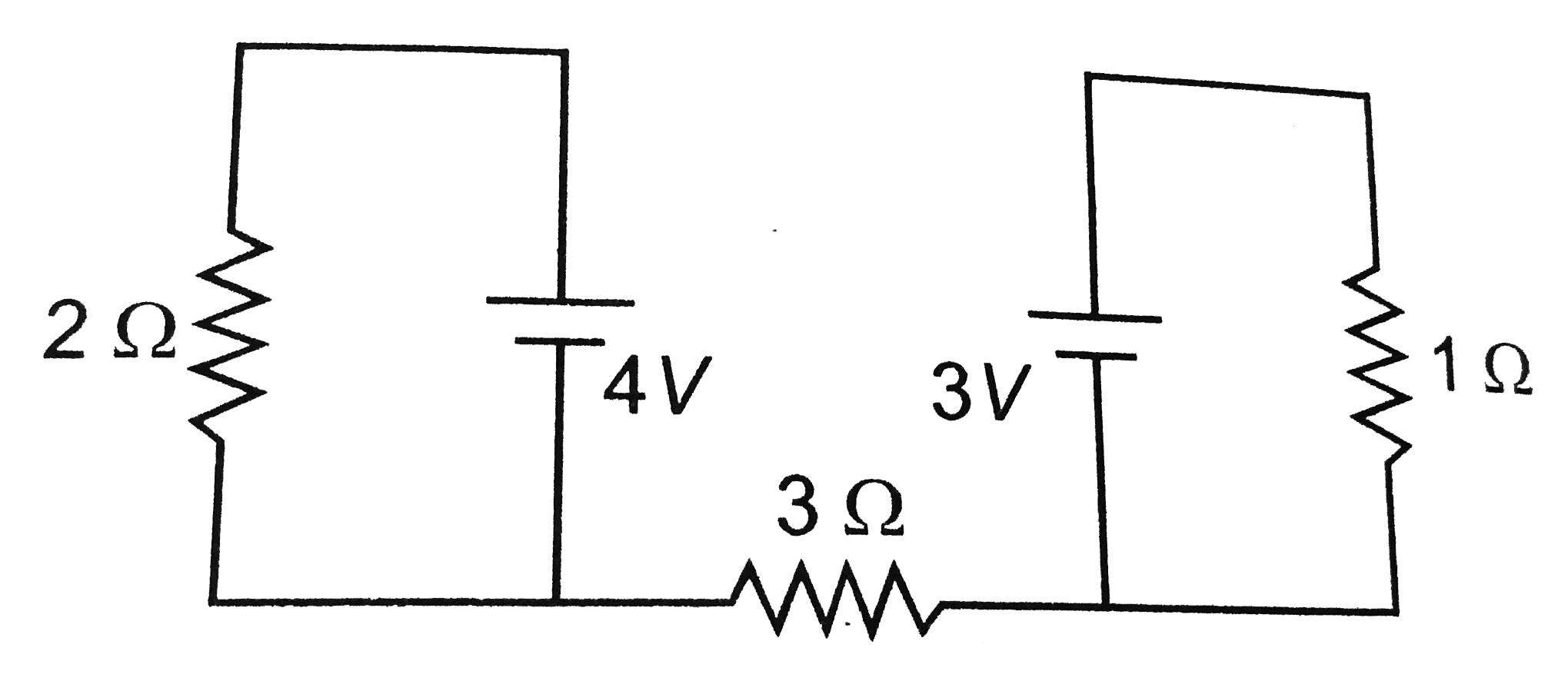
The potential drop across the 3Ω resistor is
 A1VB1.5VC2VD3V
A1VB1.5VC2VD3V
An alternating current of rms value 5A, passes through a resistance of 24Ω. What is the maximum P.D. across the resister?
View SolutionIn the circuit shown below:
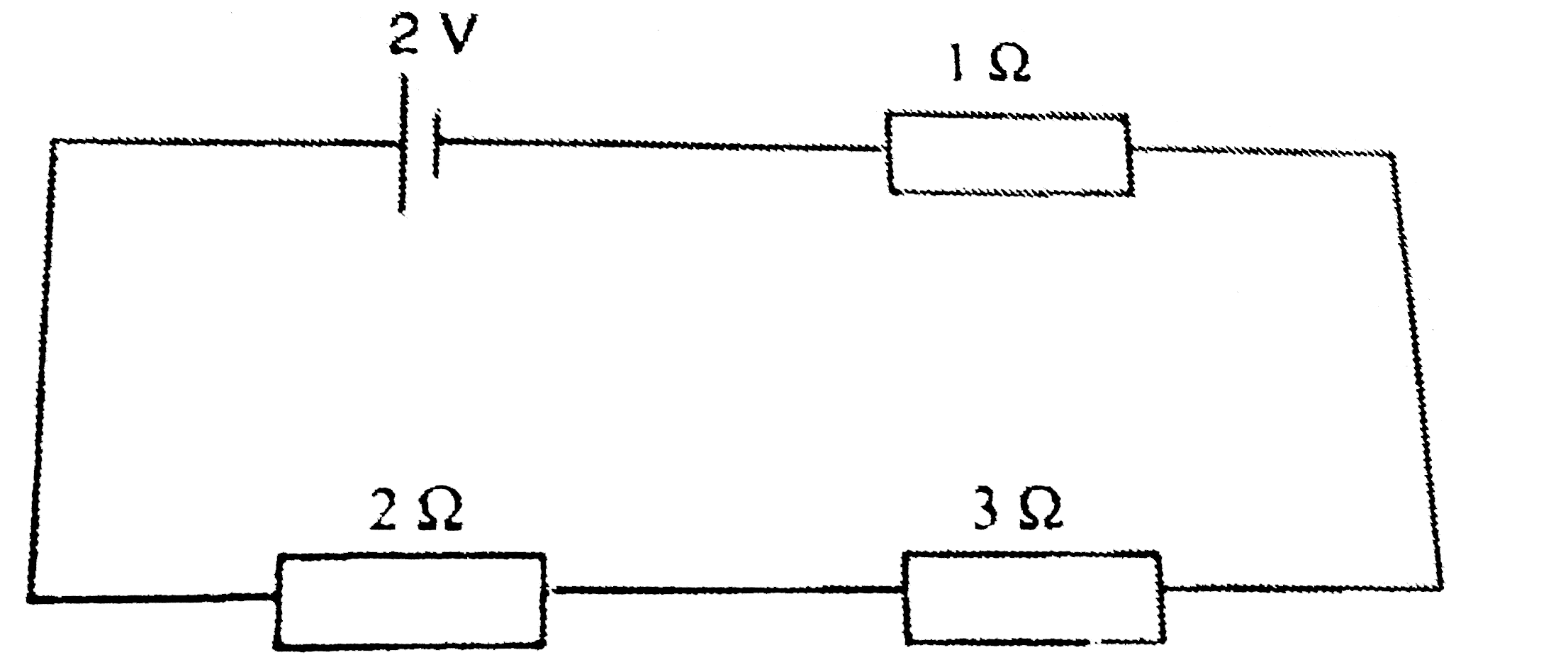
The potential difference across the 3Ω resistor is:View SolutionCurrent through the 5Ω resistor is
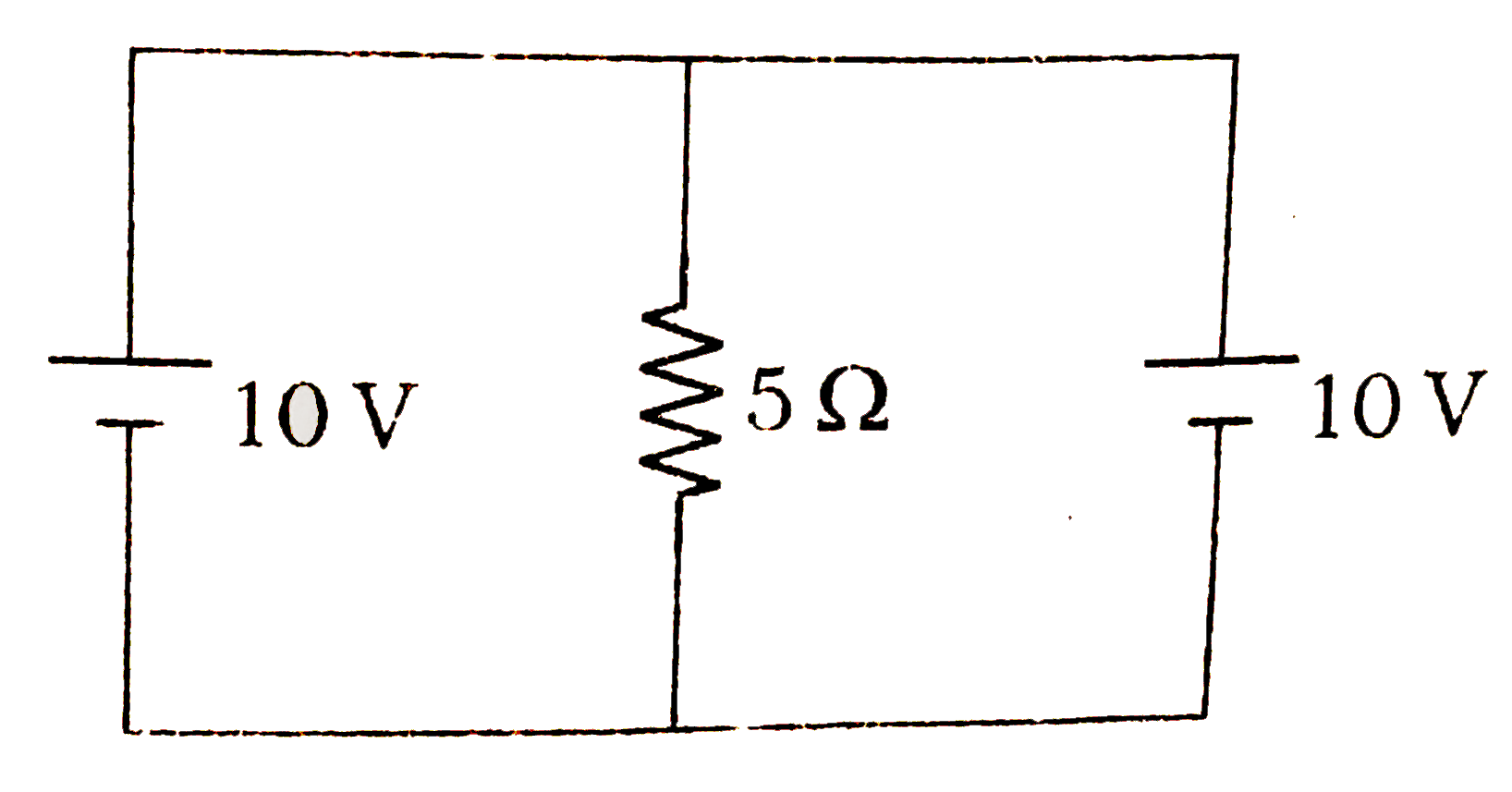 View Solution
View SolutionCurrent through 3Ω resistor is 0.8A, then potential drop through 4Ω resistor is
 View Solution
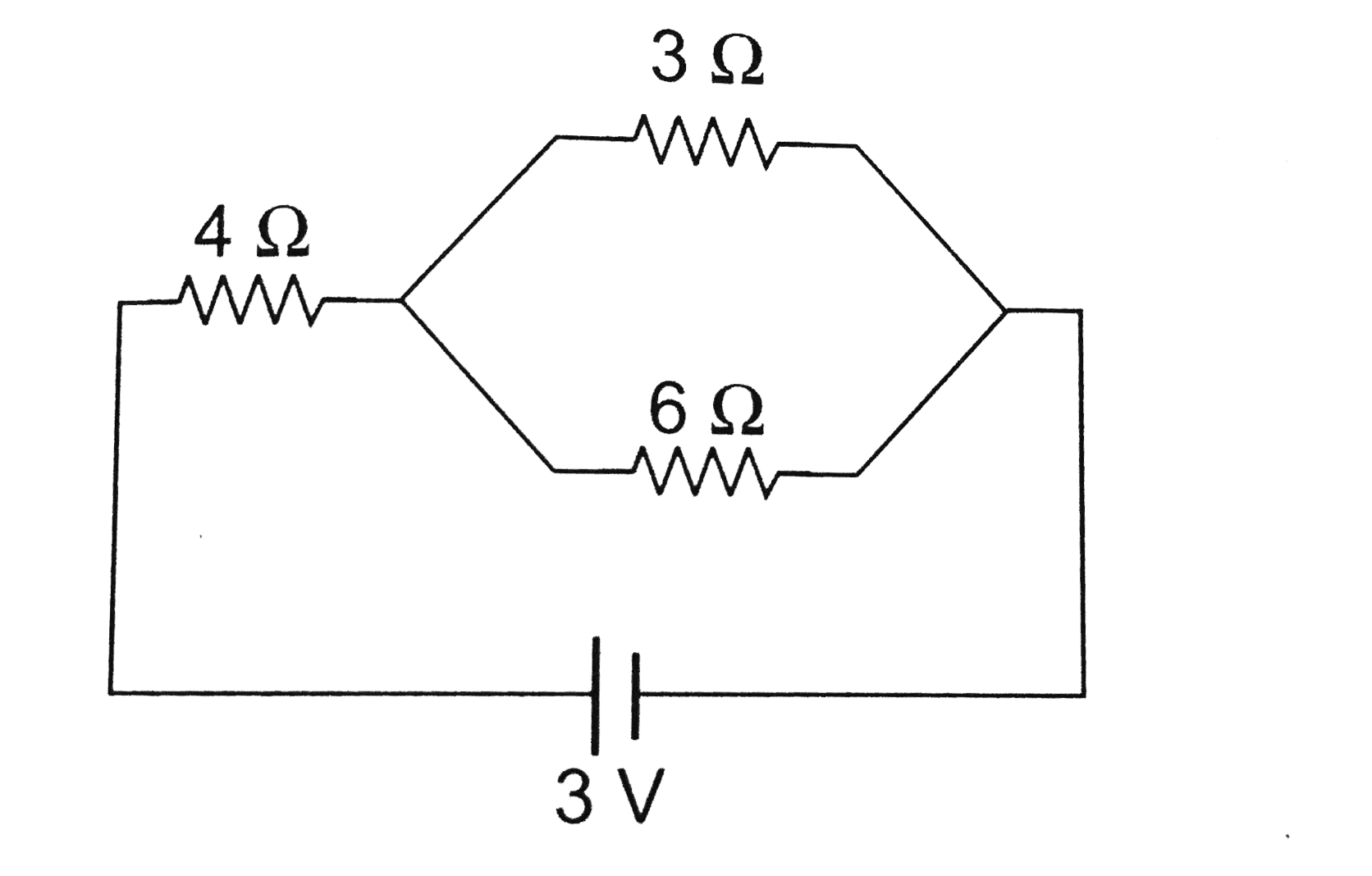
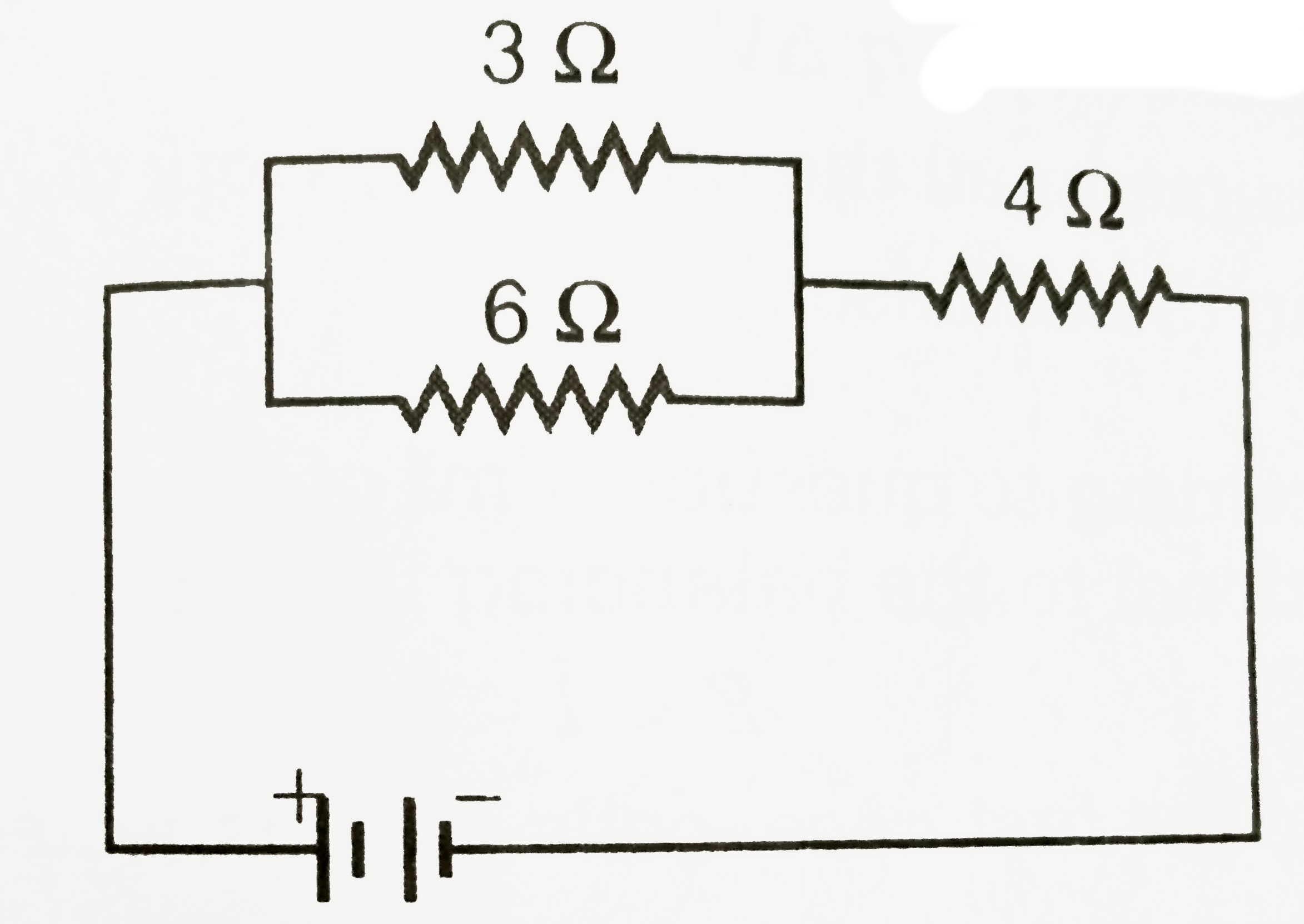
View SolutionA 3Ω resistor and a 6Ω resistor are connected in parallel and the combination is connected in series to a battery of 5 V and a 3Ω resistor. The potential difference across the 6Ω resistor
View Solution