It is necessary to write the correspondence of vertices correctly for writing congruence of triangles in symbolic form .
The correct Answer is:1
To determine whether the statement "It is necessary to write the correspondence of vertices correctly for writing the congruence of triangles in symbolic form" is true or false, we can follow these steps:
1. Understanding Congruence of Triangles:
- Congruent triangles are triangles that are identical in shape and size, meaning their corresponding sides and angles are equal.
2. Identifying Corresponding Vertices:
- When we denote two triangles, we label their vertices. For example, let’s consider triangle ABC and triangle PQR. Here, A corresponds to P, B corresponds to Q, and C corresponds to R.
3. Using the SSS Criterion:
- If we know that the sides of triangle ABC are equal to the sides of triangle PQR (i.e., AB = PQ, BC = QR, and AC = PR), we can say that triangle ABC is congruent to triangle PQR by the Side-Side-Side (SSS) criterion.
4. Writing the Congruence Statement:
- The correct way to express the congruence of these triangles symbolically is:
△ABC≅△PQR
- This notation indicates that the corresponding parts of these triangles are equal.
5. Importance of Correct Correspondence:
- If we write the congruence incorrectly, for example, stating that triangle ABC is congruent to triangle RQP, we would misrepresent the relationships between the sides and angles. This could lead to incorrect conclusions about which sides and angles are equal.
6. Conclusion:
- Therefore, it is indeed necessary to write the correspondence of vertices correctly when expressing the congruence of triangles in symbolic form. The statement is true.
- Congruent triangles are triangles that are identical in shape and size, meaning their corresponding sides and angles are equal.
- When we denote two triangles, we label their vertices. For example, let’s consider triangle ABC and triangle PQR. Here, A corresponds to P, B corresponds to Q, and C corresponds to R.
- If we know that the sides of triangle ABC are equal to the sides of triangle PQR (i.e., AB = PQ, BC = QR, and AC = PR), we can say that triangle ABC is congruent to triangle PQR by the Side-Side-Side (SSS) criterion.
- The correct way to express the congruence of these triangles symbolically is:
△ABC≅△PQR
- This notation indicates that the corresponding parts of these triangles are equal.
- If we write the congruence incorrectly, for example, stating that triangle ABC is congruent to triangle RQP, we would misrepresent the relationships between the sides and angles. This could lead to incorrect conclusions about which sides and angles are equal.
- Therefore, it is indeed necessary to write the correspondence of vertices correctly when expressing the congruence of triangles in symbolic form. The statement is true.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-B10videos
TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-C12videos
TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-A (Fill in the blanks )10videos
TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Practice Test8videos
SURFACE AREAS AND VOLUMES
Similar Questions
Knowledge Check
- Question 1 - Select One
For the given triangles, write the correspondence, if they are congruent.
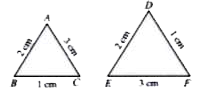 AΔABC≅ΔDEFBΔABC≅ΔEDFCΔABC≅ΔFDEDnot congruent
AΔABC≅ΔDEFBΔABC≅ΔEDFCΔABC≅ΔFDEDnot congruent
State the rules that are followed in writing SI units in symbolic form.
View SolutionGiven below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using SAS congruence rule. If the triangles are congruent, write them in symbolic form.
△ABC △DEF (a)AB=7cm,BC=5cm,∠B=50∘ DE=5cm,EF=7cm,∠E=50∘ (b)AB=4.5cm,AC=4cm,∠A=60∘ DE=4cm,FD=4.5cm,∠D=55∘ (c)BC=6cm,AC=4cm,∠B=35∘ DF=4cm,EF=6cm,∠E=35∘ View SolutionGiven below are measurements of some parts of two triangles. Examinewhether the two triangles are congruent or not, using RHS congruencerule. In case of congruent triangles, write the result in symbolic form
△ABC △PQR (i)∠B=90∘,AC=8cm,AB=3cm ∠P=90∘,PR=3cm,QR=8cm (ii)∠A=90∘,AC=5cm,BC=9cm ∠Q=90∘,PR=8cm,PQ=5cm View SolutionWhich two triangles are congruent in the given figure . Write them in symbolic form .
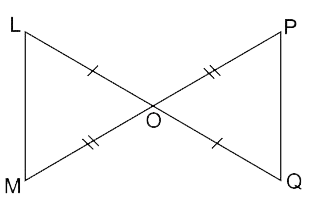 View Solution
View Solution.Which two triangles are congruent in the given figure. Write them in symbolic form.
View SolutionWhich two triangles are congruent in the given figure. Write them in symbolic form.
View SolutionLine-segments AB and CD bisect each other at O. AC and BD are joined forming triangles AOC and BOD. State the three equality relations between the parts of the two triangles that are given or otherwise known. Are the two triangles congruent? State in symbolic form, which congruence condition do you use?
View Solution

