Circle O1≅Circle O2, If radius of circle O1=6cm then diameter of circle O2 is ________
The correct Answer is:12 cm
To solve the problem, we need to find the diameter of circle O2 given that circle O1 is congruent to circle O2 and the radius of circle O1 is 6 cm.
1. Understand Congruence of Circles:
- Two circles are said to be congruent if they have the same radius.
- Therefore, if circle O1 is congruent to circle O2, it means that the radius of circle O1 is equal to the radius of circle O2.
2. Identify the Radius of Circle O1:
- We are given that the radius of circle O1 (r1) is 6 cm.
- Thus, we can write:
r1=6 cm
3. Determine the Radius of Circle O2:
- Since circle O1 is congruent to circle O2, we can conclude that the radius of circle O2 (r2) is also 6 cm.
- Therefore:
r2=r1=6 cm
4. Calculate the Diameter of Circle O2:
- The diameter (d) of a circle is calculated using the formula:
d=2×r
- Substituting the radius of circle O2 into the formula:
d2=2×r2=2×6 cm=12 cm
5. Final Answer:
- The diameter of circle O2 is:
Diameter of circle O2=12 cm
- Two circles are said to be congruent if they have the same radius.
- Therefore, if circle O1 is congruent to circle O2, it means that the radius of circle O1 is equal to the radius of circle O2.
- We are given that the radius of circle O1 (r1) is 6 cm.
- Thus, we can write:
r1=6 cm
- Since circle O1 is congruent to circle O2, we can conclude that the radius of circle O2 (r2) is also 6 cm.
- Therefore:
r2=r1=6 cm
- The diameter (d) of a circle is calculated using the formula:
d=2×r
- Substituting the radius of circle O2 into the formula:
d2=2×r2=2×6 cm=12 cm
- The diameter of circle O2 is:
Diameter of circle O2=12 cm
Topper's Solved these Questions
- TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-A (Fill in the blanks )
10 Videos
- TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-A (State which of the following statements are true and false )
5 Videos
- SURFACE AREAS AND VOLUMESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Practice Test
8 Videos
Similar Questions
Knowledge Check
If O is the centre of the circle, then x is
 A72∘B62∘C82∘D52∘
A72∘B62∘C82∘D52∘If O is the centre of the circle, then x is
 A72∘B62∘C82∘D52∘
A72∘B62∘C82∘D52∘Two tangents PA and PB are drawn from a point P to the circle. If the radius of the circle is 5 cm and AB = 6 cm and O is the centre of the circle. OP cuts AB at C and OC = 4 cm, then OP :-
A254 cmB25 cmC13 cmDNone of these
In given figure, O is the centre of the circle.
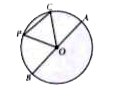
A chord, which is not the diameter of the circle is
View SolutionAB is a chord of a circle with O as centre. C is a point on the circle such that OC is perpendicular to AB and OC intersects AB at P. If PC = 2 cm and AB = 6 cm then the diameter of the circle is
View SolutionFor the four circles M, N, O and P, following four equations are given :
Circle M : x2+y2=1
Circle N : x2+y2–2x=0
Circle 0 : x2+y2−2x−2y+1=0
Circle P : x2+y2–2y=0
If the centre of circle M is joined with centre of the circle N, further centre of circle N is joined with centre of the circle O, centre of circle O is joined with the centre of circle P and lastly, centre of circle P is joined with centre of circle M, then these lines form the sides of a :
View SolutionIn Fig. 2.47, O is the centre of the circle.

Name a chord, which is not the diameter of the circle.
View SolutionAB is a tangent to a circle with centre O. If the radius at the circle is 7 cm and the length of AB is 24 cm, then what is the length (in cm) of OA?
View Solution