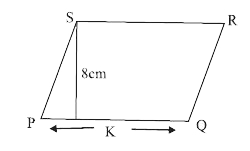
The area of a parallelogram PQRS is 36cm2. M is any point on the side RS. The area of ΔPMQ is.
18cm2
9cm2
36cm2
12cm2
The correct Answer is:A
To find the area of triangle PMQ given that the area of parallelogram PQRS is 36 cm², we can follow these steps:
1. Understand the Given Information:
- The area of parallelogram PQRS is given as 36 cm².
- M is any point on the side RS of the parallelogram.
2. Identify the Relationship:
- The area of a parallelogram can be calculated using the formula:
Area=Base×Height
- For parallelogram PQRS, we can take PQ as the base and PM as the height.
3. Set Up the Equation:
- Let the length of base PQ be b and the height PM be h.
- From the area of the parallelogram, we have:
b×h=36 cm2
4. Calculate the Area of Triangle PMQ:
- The area of triangle PMQ can be calculated using the formula:
Area of ΔPMQ=12×Base×Height
- Here, the base is PQ (which is b) and the height is PM (which is h).
- Substituting the values, we get:
Area of ΔPMQ=12×b×h
5. Substitute the Area of the Parallelogram:
- Since we know that b×h=36 cm2, we can substitute this into the triangle area formula:
Area of ΔPMQ=12×36 cm2=18 cm2
6. Final Answer:
- Therefore, the area of triangle PMQ is:
Area of ΔPMQ=18 cm2
- The area of parallelogram PQRS is given as 36 cm².
- M is any point on the side RS of the parallelogram.
- The area of a parallelogram can be calculated using the formula:
Area=Base×Height
- For parallelogram PQRS, we can take PQ as the base and PM as the height.
- Let the length of base PQ be b and the height PM be h.
- From the area of the parallelogram, we have:
b×h=36 cm2
- The area of triangle PMQ can be calculated using the formula:
Area of ΔPMQ=12×Base×Height
- Here, the base is PQ (which is b) and the height is PM (which is h).
- Substituting the values, we get:
Area of ΔPMQ=12×b×h
- Since we know that b×h=36 cm2, we can substitute this into the triangle area formula:
Area of ΔPMQ=12×36 cm2=18 cm2
- Therefore, the area of triangle PMQ is:
Area of ΔPMQ=18 cm2
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PART-A (Fill in blanks :)18videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-B5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE TEST3videos
CIRCLES
Similar Questions
Knowledge Check
- Question 1 - Select One
PQRS is a parallelogram whose area is 180cm2 and A is any point on the diagonal QS. The area of ΔASR?
AEqual to 90cm2BGreater than 90cm2CLess than 90cm2DNone of these - Question 2 - Select One
One side of a parallelogram is 14 cm.Its distance from the opposite side is 16 cm.The area of parallelogram is -----
A112 sq.cmB224 sq .cmC56π sq.cmD210 sq.cm - Question 3 - Select One
The area of an equilateral triangle is 36√3cm2. Find its side (in cm).
A6B24C12D36
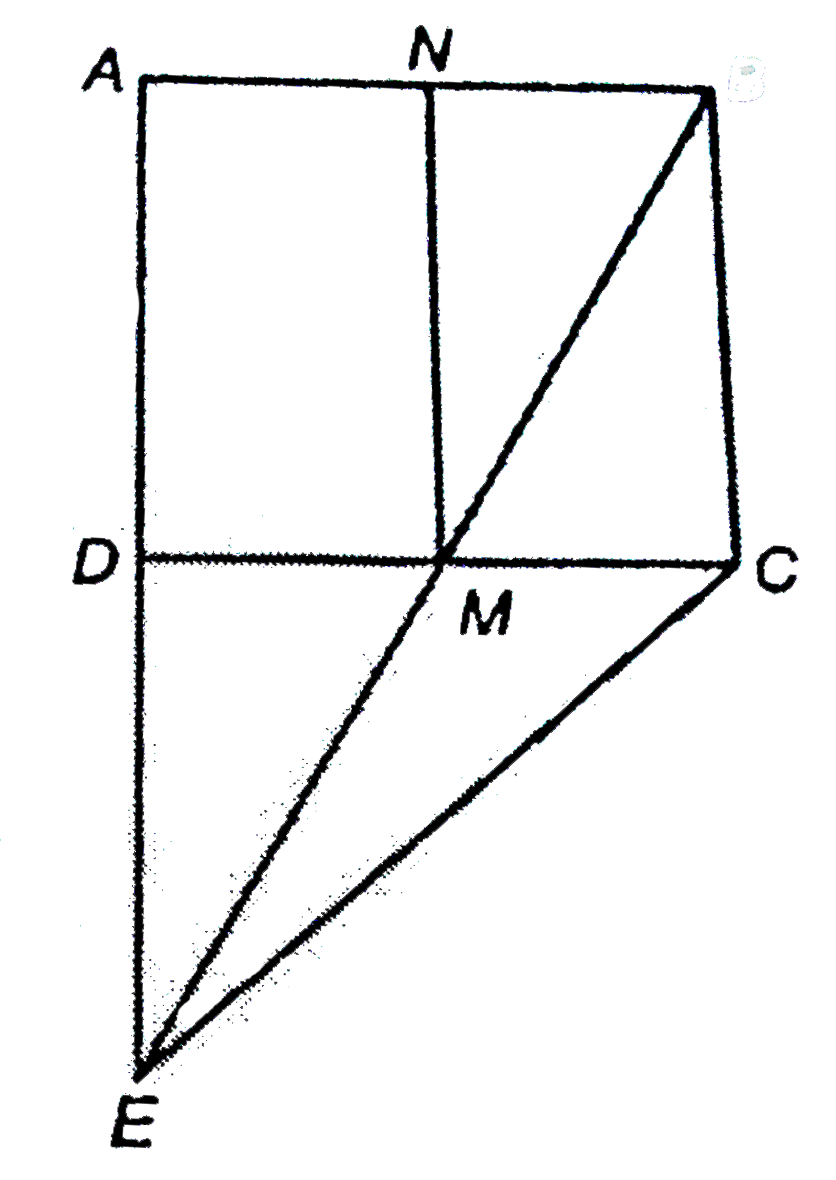
In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD. If the area of parallelogram is 48cm2
(i) State the area of ΔBEC
(ii) Name the parallelogram which is equal in area to the triangle BEC.
 View Solution
View SolutionOne side of a parallelogram is 16 cm and the distance of this side from the opposite side is 4.5 cm. The area of the parallelogram is
View SolutionOne side of a parallelogram is 14 cm. Its distance from the opposite side is 16.5 cm. Find the area of the parallelogram
View SolutionThe area of an equilateral triangle is 36√3cm2. Find its side (in cm).
View SolutionOne side of a parallelogram is 14 cm and the distance of this side from the opposite side is 6.5 cm. The area of the parallelogram is
View Solution