M, A and P are the mid-points of the sides DE, DF and EF of Δ DEF respectively. Which of the following statements is true ?
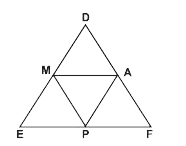
ar (ΔMPF)=2 ar (ΔDEF)
ar (AMPF)=12 ar (ΔDEF)
ar (ΔAMP)=14 ar (ΔDEF)
ar (AMPF)=12 ar (ΔDEF)
The correct Answer is:B
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PART-A (Fill in blanks :)
18 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-B
5 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE TEST
3 Videos
Similar Questions
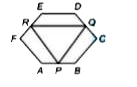
In the given figure, ABCDEF is a regular hexagon of side 12cm. P, Q and R are the mid points of the sides AB, CD and EF respectively. What is the area (in cm2) of triangle PQR ?
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :

View Solution
Knowledge Check
M, A and P are the mid-points of the sides DE, DF and EF of Δ DEF respectively. Which of the following statements is true ?
 Aar (ΔMPF)=2 ar (ΔDEF)Bar (AMPF)=12 ar (ΔDEF)Car (ΔAMP)=14 ar (ΔDEF)Dar (AMPF)=12 ar (ΔDEF)
Aar (ΔMPF)=2 ar (ΔDEF)Bar (AMPF)=12 ar (ΔDEF)Car (ΔAMP)=14 ar (ΔDEF)Dar (AMPF)=12 ar (ΔDEF)ΔDEF is divided into two triangles ΔDEMandΔDFM of equal areas. Which of the following statement is true ?
AΔDEFandΔDFM have equal bases.Bar (ΔDEM)=13 ar (ΔDEF)CMis the mid - point of side EF.DΔDEMandΔDFM and congruent.If ΔABC~ΔDEF, then which of the following is true?
ABC.EF = AC.FDBAB.ED = AC.DECBC.DE = AB.EFDBC.DE = AB.FD
D, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
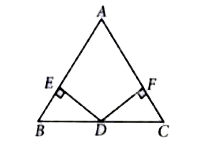
View SolutionIn the given figure, is the mid point of BC, DE ⊥ AB and DF⊥AC such that DE= DE. Then, which of the following is true?
View SolutionIf D, E and F are the mid-points of the sides of an equilateral triangle ABC, then the ratio of the area of triangle DEF and DCF is :
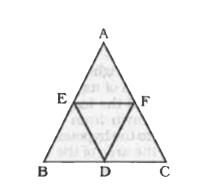
View SolutionIf D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
View Solution
