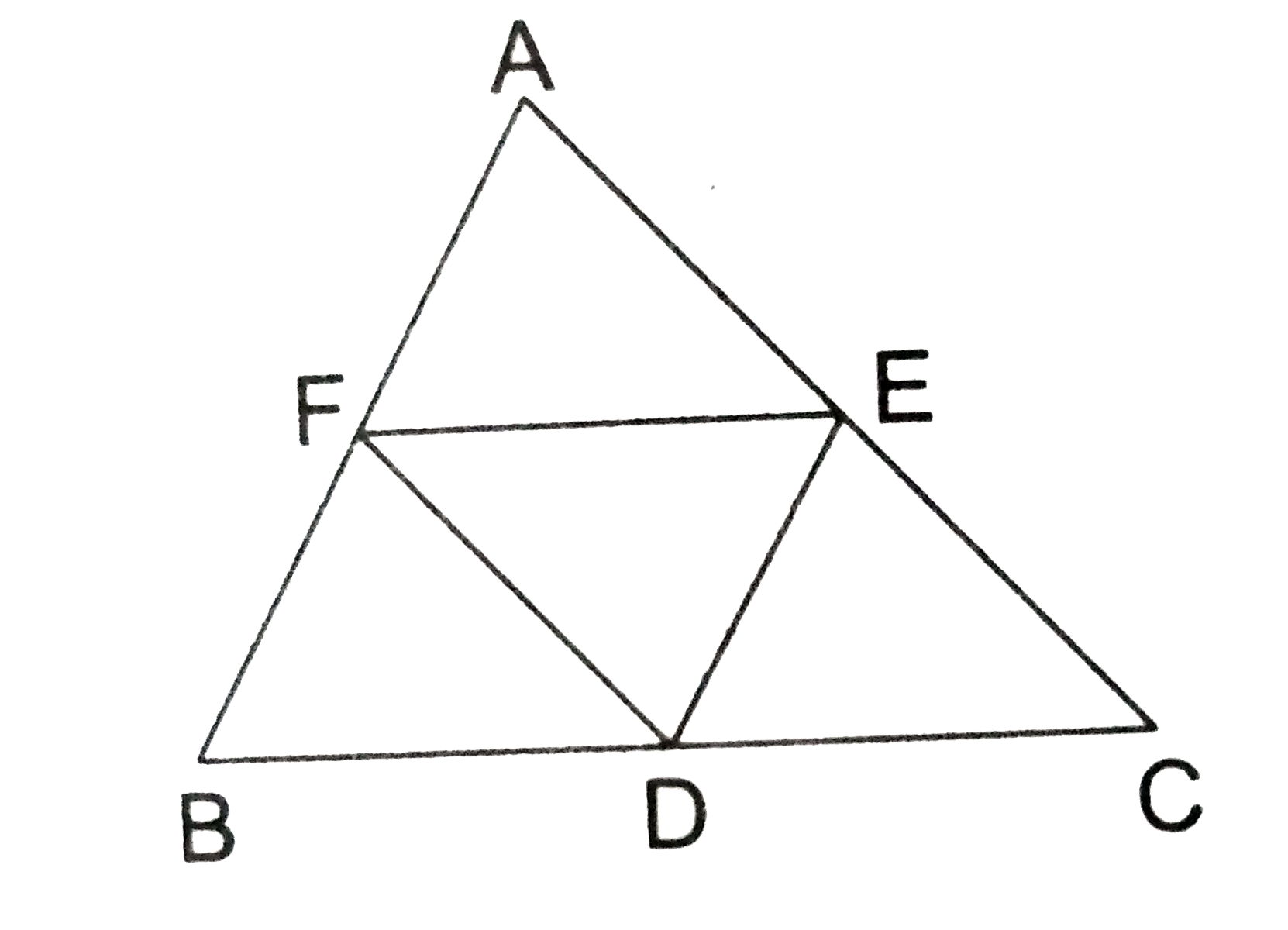
D, E and F are respectively the mid -points of the sides BC, CA and AB of a △ABC .Show that (i) BDEF is a parallelogram
The correct Answer is:16ΔABC
Step by step video, text & image solution for D, E and F are respectively the mid -points of the sides BC, CA and AB of a triangleABC .Show that (i) BDEF is a parallelogram by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-C
3 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-D
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PART-A (Fill in blanks :)
18 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE TEST
3 Videos
Similar Questions
D, E and F are respectively the mid-points of the sides BC, CA and AB of aΔABC.Show that (i) BDEF is a parallelogram. (ii) ar (DEF)=14ar (ABC)(iii) ar (BDEF)=12ar (ABC)
View SolutionD, E and F are respectively the mid -points of the sides BC, CA and AB of a △ABC .Show that (i) BDEF is a parallelogram
View Solution
Knowledge Check
If D, E and F are respectively the mid - points of sides BC, AC and AB of a ΔABC. If EF=3cm,FD=4cm and AB=10cm, then DE,BCandCA respectively will be equal to :
A6, 8 and 20 cmB4, 6 and 8 cmC5, 6 and 8 cmD10/3, 9 and 12 cm
D, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(BDEF) =12ar(△ABC)
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) area of □BDEF=12× area of ΔABC

View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC. Prove that
(i) BDEF is a ||gm,
(ii) ar(△DEF)=14ar(△ABC)and
(iii) ar(||gm BDEF)=12ar(△ABC)
View Solution
