Let x be the class mark & y be the upper limit of a class-interval in a continuous frequency-distribution.
The lower limit of the class is:
2x+y
2x-y
x-y
x+y
The correct Answer is:B
To find the lower limit of a class interval in a continuous frequency distribution, we can follow these steps:
1. Understand the Definitions:
- Let x be the class mark.
- Let y be the upper limit of the class interval.
- We need to find the lower limit, which we will denote as L.
2. Class Mark Formula:
- The formula for the class mark x is given by:
x=L+y2
- This formula states that the class mark is the average of the lower limit L and the upper limit y.
3. Rearranging the Formula:
- To find L, we can rearrange the formula:
L+y=2x
- This means that the sum of the lower limit and the upper limit equals twice the class mark.
4. Isolating the Lower Limit:
- Now, we isolate L by subtracting y from both sides:
L=2x−y
5. Final Expression:
- Thus, the lower limit L of the class interval is given by:
L=2x−y
Conclusion:
The lower limit of the class interval is 2x−y.
---
- Let x be the class mark.
- Let y be the upper limit of the class interval.
- We need to find the lower limit, which we will denote as L.
- The formula for the class mark x is given by:
x=L+y2
- This formula states that the class mark is the average of the lower limit L and the upper limit y.
- To find L, we can rearrange the formula:
L+y=2x
- This means that the sum of the lower limit and the upper limit equals twice the class mark.
- Now, we isolate L by subtracting y from both sides:
L=2x−y
- Thus, the lower limit L of the class interval is given by:
L=2x−y
The lower limit of the class interval is 2x−y.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - PART B9videos
STATISTICS
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - PART C3videos
STATISTICS
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - QUARILATERAL EXERCISE - Part - D5videos
QUARILATERAL
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Practice Test8videos
SURFACE AREAS AND VOLUMES
Similar Questions
Knowledge Check
- Question 1 - Select One
Let m be the mid - point and l the upper class limit of a class in a continuous frequency distribution The lowe limit of the class is
A2m+lB2m−lCm−lDm−2l - Question 2 - Select One
If m is the mid-point and l is the upper limit of a class in a continous frequency distribution, then lower class limit of the class is
A2m+lB2m−lCm−lDm−2l - Question 3 - Select One
Consider the frequency distribution.

The upper limit of median class isA17B17.5C18D18.5
Consider the following frequency distribution:

the upper limit of the median class isView SolutionLet l be the lower class limit of a class-interval in a frequency distribution and m be the mid-point of the class. Then, the upper class limit of the class is m+l+m2 (b) l+m+12 (c) 2m−l (d) (m−2l)
View SolutionFind the lower limit of the median class
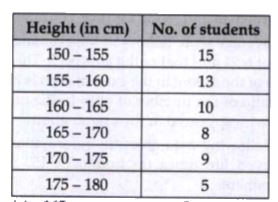 View Solution
View SolutionConsider the following frequency distribution

The upper limit of the median class inView SolutionFor the following distribution

the lower limits of the modal class isView Solution


