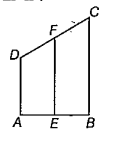
ABCD is trapezium in which AB∣∣DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
ar(DCYX)=79ar(XYBA).
The correct Answer is:A, B, C, D
Step by step video, text & image solution for ABCD is trapezium in which AB||DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that ar (DCYX) = (7)/(9) ar (XYBA). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE TEST QUESTION PAPER 1EXERCISE - SECTION-D5videos
PRACTICE TEST QUESTION PAPER 1
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE TEST QUESTION PAPER 1EXERCISE - SECTION-B4videos
PRACTICE TEST QUESTION PAPER 1
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICE QUESTION PAPER-2EXERCISE - PART D7videos
PRACTICE QUESTION PAPER-2
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PRACTICES QUESTION PAPER -3EXERCISE - PART D5videos
PRACTICES QUESTION PAPER -3
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=A40 cmB50 cmC60 cmD30 cm - Question 2 - Select One
ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
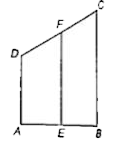 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2 - Question 3 - Select One
ABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
A80∘B100∘C120∘D140∘
In the given figure ABCD is a trapezium with AB || DC. E and F are respectively midpoint of AD and BC. Prove that, EF=12(AB+CD)
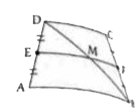 View Solution
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
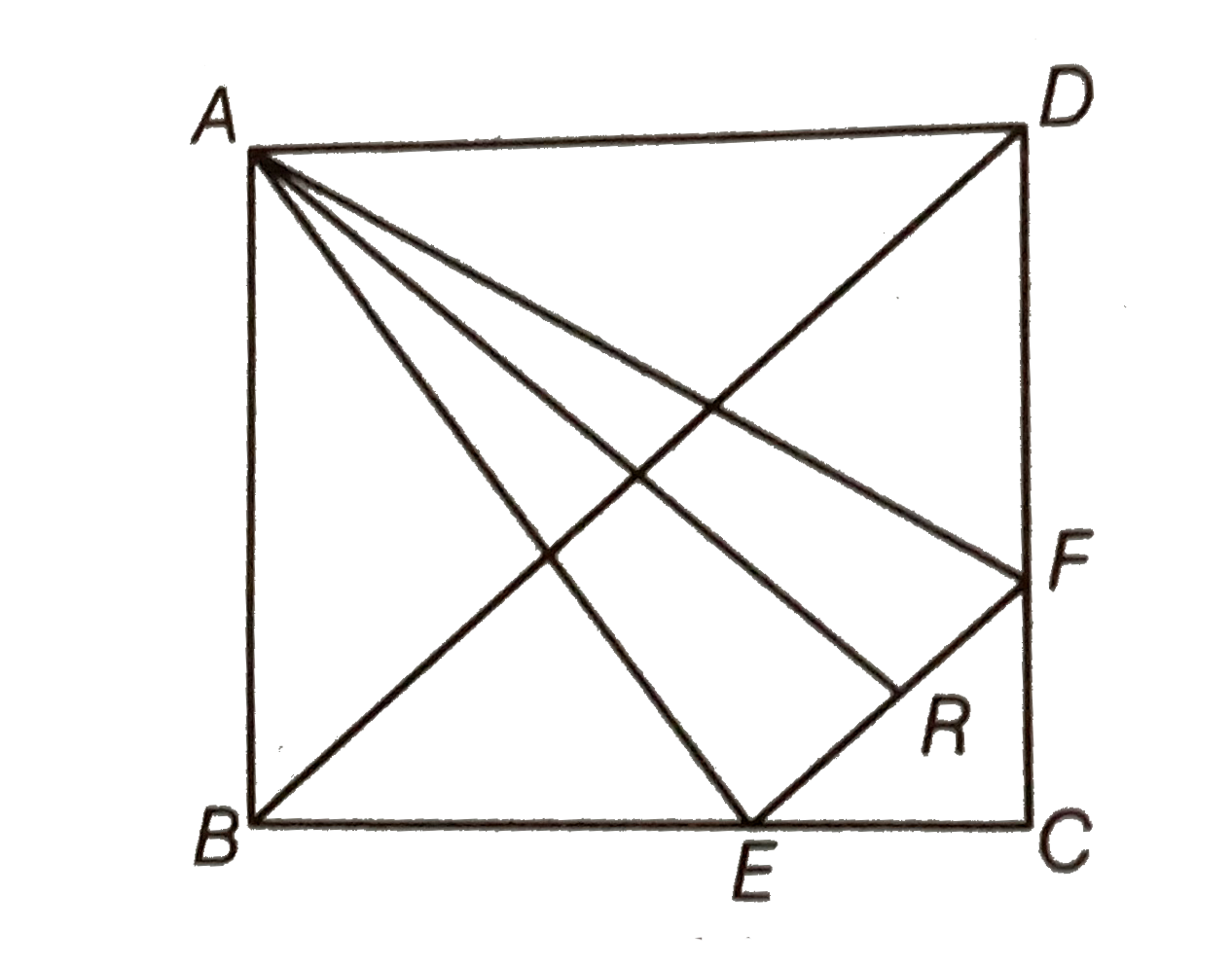 View Solution
View SolutionABCD is a trapezium in which AB || DC, ABデ78 cm, CD = 52 cm. AD = 28 cm and BC =30cm . Find the area of the trapezium.
View SolutionABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
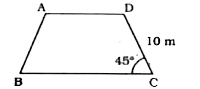 View Solution
View SolutionABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
View Solution