If the roots of the equation q2x2+p2x+r2=0 are the squares of the roots of the equation qx2+px+r=0, are the squares of the roots of the equation qx2+px+r=0, then q, p, r are in: Solution in Tamil
A.P
G.P
Both A.P and G.P
None of these
The correct Answer is:B
Step by step video, text & image solution for If the roots of the equation q^(2)x^(2)+p^(2)x+r^(2)=0 are the squares of the roots of the equation qx^(2)+px+r=0, are the squares of the roots of the equation qx^(2)+px+r=0, then q, p, r are in: by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ALGEBRABook:PREMIERS PUBLISHERSChapter:ALGEBRAExercise:SOLUTION TO UNIT EXERCISE
Explore 23 Videos
- ALGEBRABook:PREMIERS PUBLISHERSChapter:ALGEBRAExercise:SOLUTION THINKING CORNER
Explore 6 Videos
- ALGEBRABook:PREMIERS PUBLISHERSChapter:ALGEBRAExercise:SOLUTION TO EXERCISE 3.18
Explore 15 Videos
- CO-ORDINATE GEOMETRY Book:PREMIERS PUBLISHERSChapter:CO-ORDINATE GEOMETRY Exercise:Other Important Objective
Explore 25 Videos
Similar Questions
Solve 13(x+y−5)=y−z=2x−11=9−(x+2z).
View SolutionThe number of possible solutions when solving system of linear equations in three variables are ……………..
View SolutionFind the order of the product matrix AB is
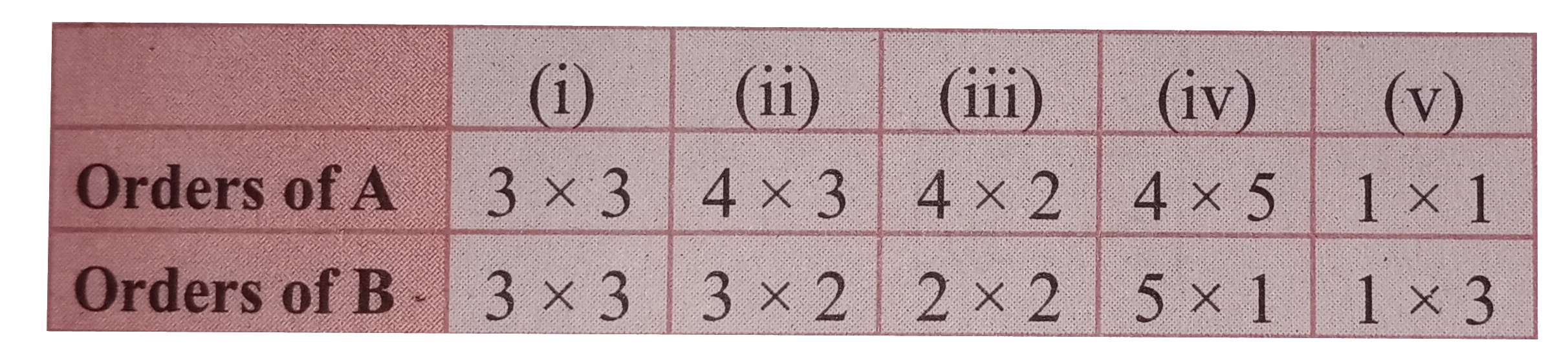
View SolutionThe area of the triangle formed by the points (0,0),(3,0) and (0,4) is :
View SolutionIf p,q,r in R and the quadratic equation px^(2)+qx+r=0 has no real root,then
View SolutionIf alpha,beta are the roots of the equation px^(2)-qx+r=0, then the equation whose roots are alpha^(2)+(r)/(p) and beta^(2)+(r)/(p) is (i) p^(3)x^(2)+pq^(2)x+r=0 (ii) px^(2)-qx+r=0 (iii) p^(3)x^(2)-pq^(2)x+q^(2)r=0 (iv) px^(2)+qx-r=0
View SolutionIf the equations px^(2)+qx+r=0 and rx^(2)+qx+p=0 have a negative common root then the value of (p-q+r)=
View SolutionIf the roots of the equation x3−px2+qx−r=0 are in A.P., then
View SolutionFind the sum of the squares and the sum of the cubes of the roots of the equations x3−px2+qx−r=0 in terms of p,q,r
View SolutionShow that the equations px2+qx+r=0 and qx2+px+r=0 will have a common root if p+q+r=0 or, p=q=r.
View SolutionIf the roots of the equation q2x2+p2x+r2=0 are the squares of the roots of the equation qx2+px+r=0 then q, p, r are in ___.
View SolutionIf the roots of the equation q2x2+p2x+r2=0 are the squares of the roots of the equation qx2+px+r=0 , then p,q,r are in ………………….. .
View SolutionIf p,q,r are in A.P. and are positive, the roots of the quadratic equation px2+qx+r=0 are real for :
View SolutionShow that the roots of the equation
x3+px2+qx+r=0 are in
G.P p3r=q3
View SolutionIf p, q, r are positive and are in AP, the roots of quadratic equation px2+qx+r=0 are real for :
View Solution
