Every section of a sphere by a plane is a ………
The correct Answer is:circle
Topper's Solved these Questions
- MENSURATIONBOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - SOLUTION TO ACTIVITIES
11 Videos
- MENSURATIONBOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
16 Videos
- MENSURATIONBOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - SOLUTION TO THINKING CORNER
25 Videos
- GEOMETRYBOOK - PREMIERS PUBLISHERSCHAPTER - GEOMETRYEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
22 Videos
- NUMBERS AND SEQUENCESBOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS
23 Videos
Similar Questions
Knowledge Check
Section of a sphere by a plane.
(a) x2+y2+z2+2vy+2wz+d=09 represent a sphere with center at (−u,−v,−w) and r=√u2+v2+w2−d
The section of a sphere by a plane is a circle.If its redius be a than a=√u2+v2+w2−d
(b) The section of a sphere by a plane is a circle. If its radius be a then a=√r2−p2, where p mis perpendiculer from center to given plane.

if the plane passes through the center of the sphere, then this section is called great circle.
In this case p=0 ∴ a=r,i.e., its center and radius is this case p=0 ∴ a=r,i.e., its centre and radius is the same as of given sphere
If S=0andp=0 be the equations of a sphere and a plane, then s+γP=0 represents a sphere through the circle S=0,P=0
The equation of a sphere passing through origin and the points, (a,0,0),(0,b,0)and(0,0,c)
Or
The plane x/a+y/b+z/c=1 meets the co-ordinate axes in the points A,B,C and O be the origin. The sphere OABC isAx2+y2+z2+ax+by+cz=0Bx2+y2+z2=a+b+c=0Cx2+y2+z2−2ax−2by−2cz=0Dx2+y2+z2−ax−by−cz=0Section of a sphere by a plane.
(a) x2+y2+z2+2vy+2wz+d=09 represent a sphere with center at (−u,−v,−w) and r=√u2+v2+w2−d
The section of a sphere by a plane is a circle.If its redius be a than a=√u2+v2+w2−d
(b) The section of a sphere by a plane is a circle. If its radius be a then a=√r2−p2, where p mis perpendiculer from center to given plane.

if the plane passes through the center of the sphere, then this section is called great circle.
In this case p=0 ∴ a=r,i.e., its center and radius is this case p=0 ∴ a=r,i.e., its centre and radius is the same as of given sphere
If S=0andp=0 be the equations of a sphere and a plane, then s+γP=0 represents a sphere through the circle S=0,P=0
The equation of the sphere touching the three co-ordinate planes isA∑x2+(x+y+z)+2a2=0B∑x2−(x+y+z)+2a2=0C∑x2±(x+y+z)+2a2=0D∑x2±2ax±2ay±2az±2a2=0Section of a sphere by a plane.
(a) x2+y2+z2+2vy+2wz+d=09 represent a sphere with center at (−u,−v,−w) and r=√u2+v2+w2−d
The section of a sphere by a plane is a circle.If its redius be a than a=√u2+v2+w2−d
(b) The section of a sphere by a plane is a circle. If its radius be a then a=√r2−p2, where p mis perpendiculer from center to given plane.

if the plane passes through the center of the sphere, then this section is called great circle.
In this case p=0 ∴ a=r,i.e., its center and radius is this case p=0 ∴ a=r,i.e., its centre and radius is the same as of given sphere
If S=0andp=0 be the equations of a sphere and a plane, then s+γP=0 represents a sphere through the circle S=0,P=0
The co-ordinates of the center and the radius of the circle x+2y+2z=15,x2+y2+z2−2y−4z=11 areA(4,3,1),√5B(3,4,1),√6C(1,3,4),√7DNone
A sphere of weight w=100N is kept stationary on a rought inclined plane by a horizontal string AB as shown in figure. Find
(a)tension in the string,
(b) force of friction on the sphere and
(c)normal reation on the sphere by the plane.
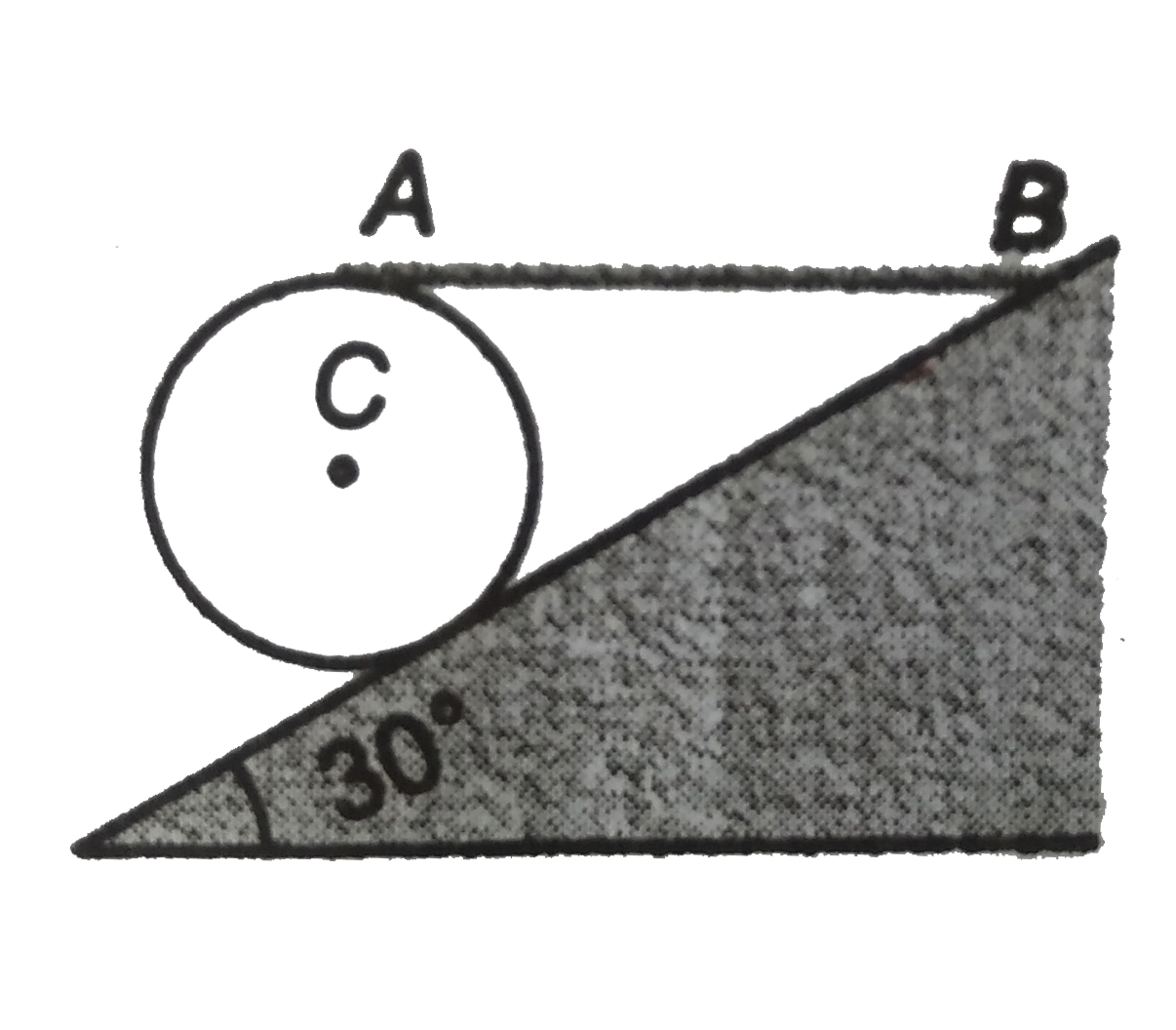
View SolutionA sphere of weight w=100N is kept stationary on a rought inclined plane by a horizontal string AB as shown in figure. Find
(a)tension in the string,
(b) force of friction on the sphere and
(c)normal reation on the sphere by the plane.

View SolutionWhat is the locus of points of intersection of a sphere and a plane ?
View SolutionWhat is the locus of points of intersection of a sphere and a plane?
View SolutionIn a right circular cone, the cross - section made by a plane parallel to the base is a (A) Circle (B) Frustum of a cone (C) Sphere (D) Hemisphere
View Solution
