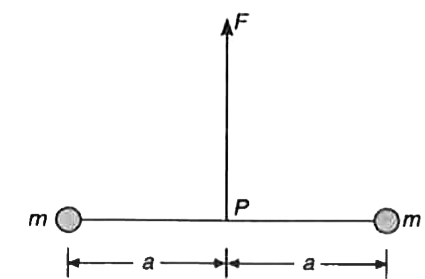
दो कण , जिनमें से प्रत्येक का द्रव्यमान m है , 2a लम्बाई की एक हल्की डोरी के किनारों पर बंधे है। यह संपूर्ण निकाय एक घर्षणहीन क्षैतिज तल पर इस प्रकार रखा है कि डोरी तनी हुई है , तथा प्रत्येक कण डोरी के मध्य - बिन्दु P से a दूरी पर है। अब डोरी के मध्य - बिन्दु को उर्ध्वाधर दिशा में ऊपर को ओर एक लघु , किन्तु एकसमान परिमाण के बल F से खींचा जाता है। परिणामस्वरूप , कण क्षैतिज तल पर एक - दूसरे की ओर चलने लगते है। जब कणों के बीच की दूरी 2x हो जाती है , तब उनके त्वरणों का परिणाम है-
 .
.
F2m.a√a2−x2
F2m.x√a2−x2
F2m.xa
F2m.√a2−x2x
The correct Answer is:B
मान जब कणों के बीच दूरी 2x है , तब प्रत्येक डोरी में तनाव T है। T को ऊर्ध्व तथा क्षैतिज अवयवों में लिखने पर 2Tsinθ=F तथा Tcosθ=max,
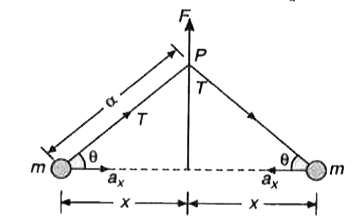
जहाँ ax प्रत्येक कण का क्षैतिज दिशा में त्वरण है। इन समीकरणों से 2tanθ=Fmax अथवा ax=F2mtanθ
चित्र से , tanθ=√a2−x2x∴ax=F2mx√a2−x2.
ऊर्ध्व त्वरण ay=F2m अति लघु होने के कारण नगण्य है। अतः प्रत्येक कण का परिणामी त्वरण ax ही माना जा सकता है।
Topper's Solved these Questions
- गति के नियम BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गति के नियम EXERCISE - बहुविकल्पीय प्रश्न II
4 Videos
- गति के नियम BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गति के नियम EXERCISE - सत्य /असत्य
4 Videos
- कार्य ऊर्जा एव सामर्थ्य BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
6 Videos
- गुरुत्वाकर्षण BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गुरुत्वाकर्षण EXERCISE - विश्लेषणात्मक प्रश्न
5 Videos
Similar Questions
L लम्बाई तथा M द्रव्यमान (गोलक) का एक सरल लोलक एक समतल में उर्ध्वाधर रेखा के परितः (−ϕ) तथा (+ϕ) कोणीय सीमाओं के मध्य दोलन करता है। कोणीय विस्थापन θ(|θ|<ϕ) के लिए डोरी में तनाव तथा गोलक का वेग क्रमशः T तथा v है। इन परिस्थियों के अंतर्गत निम्न सम्बन्ध सही है।
View Solutionजब कोई व्यक्ति किसी रुक्ष तल पर चलता है तो पृष्ठ द्वारा व्यक्ति पर आरोपित घर्षण बल की दिशा व्यक्ति की गति के विपरीत होती है।
View Solutionएक नत समतल के घर्षण रहित पृष्ठ पर M द्रव्यमान का एक छोटा गुटका गतिमान है, बिंदु B पर नत समतल का कोण 60∘से 30∘ अचानक परिवर्तित होता है। गुटका प्रारम्भ में बिंदु A पर विरामावस्था में है। नत समतल तथा गुटके के बिच संघट्ट अप्रत्यास्थ माना गया (g=10मीसे2)
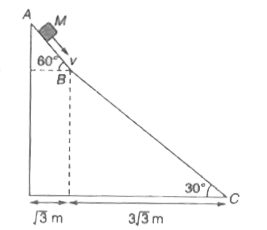
दूसरे नत समतल से टकराने के तुरंत बाद बिंदु B पर गुटके की चाल है
View Solutionदो उपग्रह S1 व S2 एक ग्रह के चारों ओर समतलीय वृत्ताकार कक्षाओं में एक ही दिशा में घूमते हैं। उनके परिक्रमण काल क्रमश: 1 घण्टा व 8 घण्टा हैं। S1 की कक्षा की त्रिज्या 104 किमी है। जब S2,S1 के निकटस्थ है तो ज्ञात कीजिए (a) S1 के सापेक्ष S2 की चाल, (b) S1 में बैठे अन्तरिक्ष यात्री द्वारा वास्तविक रूप से प्रेक्षित S2 की कोणीय चाल।
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionएक कम्पनी दो प्रकार के टेलीफोनों का निर्माण करती है|पहला डोरी युक्त,दूसरा डोरी रहित| डोरी युक्त टेलीफ़ोन के निर्माण में 2 घंटे लगते है तथा रहित डोरी मॉडल के निर्माण में 4 घंटे लगते है| कम्पनी के पास इन प्रतिरूपों के निर्माण के लिए प्रतिदिन अधिक से अधिक 800 कार्य घंटे उपलब्ध है तथा पैकिंग विभाग प्रतिदिन अधिक से अधिक 300 टेलीफ़ोन सेटों को पैक कर सकता है|यदि कम्पनी डोरी युक्त मॉडल को रु 300 में बेचती है तथा डोरी रहित मॉडल को रु 400 में बचती है ,तो उसे प्रत्येक प्रकार के कितने टेलीफ़ोन सेल प्रतिदिन निर्मित करने चाहिए जिससे की उसकी बिक्री अधिकतम हो?
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solution
