द्रव्यमान m की एक गोलाकार गेंद दो स्थिर, सकेंद्रित गोलों A तथा B के बीच के स्थान में उच्चतम बिंदु पर रखी गई है। छोटे गोले A की त्रिज्या R है, तथा दोनों गोलों के बीच के स्थान के चौड़ाई d है गेंद का व्यास, d से थोड़ा कम है। सभी तल घर्षणहीन है। गेंद को एक हल्का-सा धक्का दे और दिया जाता है। गेंद का त्रिज्य वेक्टर, उर्ध्वार्धर से θ कोण बनाता है
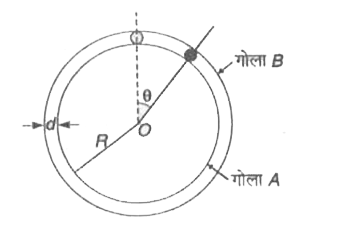
(a) गोलों द्वारा गेंद पर आरोपित अभिलम्ब प्रतिक्रिया बल, कोण θ के फलन के रूप में व्यक्त कीजिए।
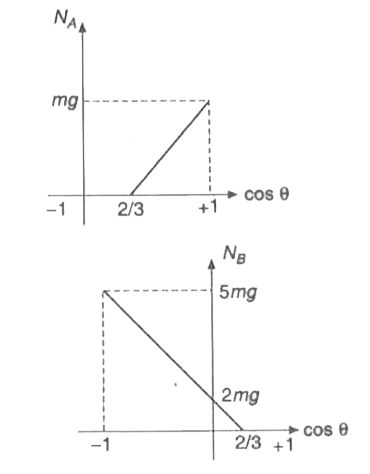
(b) माना गोलों A तथा B द्वारा गेंद पर आरोपित अभिलम्ब प्रतिक्रिया के परिमाण क्रमशः NA तथा NB है। NA तथा NB के विचारणो को 0≤θ≤π परास में, cosθ के फलन के रूप में (cosθ क्षैतिज अक्ष के अनुदिश दो अलग-अलग लेखाचित्रो द्वारा दिखाइए।
ज्यामिति से h=(R+d2)(1−cosθ)
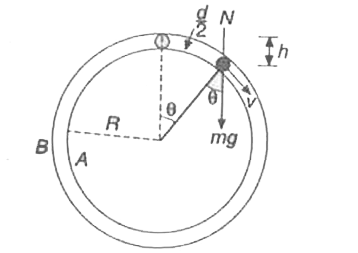
वजा संरक्षण के नियम से,
गतिज ऊर्जा = स्थितिज ऊर्जा
12mv2=mg(R+d2)(1−cosθ)
v2=2gh=2(R+d2)(1−cosθ)g ...(i)
माना θ कोण पर (केंद्र से दूर) कुल अभिलम्ब ज्प्रतिक्रिया न है, तब (mgcosθ−N) अभिकेंद्र बल के बराबर होगा। mgcosθ−N=mv2(R+d2)
(v2 का मान प्रतिस्थापित करने पर )
mgcosθ−N=2mg(1−cosθ)
या N=mg(3cosθ−2)
Topper's Solved these Questions
- कार्य ऊर्जा एव सामर्थ्य BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
6 Videos
- कार्य ऊर्जा एव सामर्थ्य BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - एकल पूर्णक उत्तर प्रकार
4 Videos
- ऊष्मा एवं उष्मागतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - ऊष्मा एवं उष्मागतिकी EXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- गति के नियम BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गति के नियम EXERCISE - श्रृंखलाबद्ध -बोधन प्रकार
2 Videos
Similar Questions
एक नत समतल के घर्षण रहित पृष्ठ पर M द्रव्यमान का एक छोटा गुटका गतिमान है, बिंदु B पर नत समतल का कोण 60∘से 30∘ अचानक परिवर्तित होता है। गुटका प्रारम्भ में बिंदु A पर विरामावस्था में है। नत समतल तथा गुटके के बिच संघट्ट अप्रत्यास्थ माना गया (g=10मीसे2)
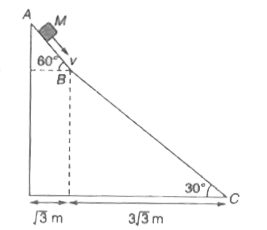
दूसरे नत समतल से टकराने के तुरंत बाद बिंदु B पर गुटके की चाल है
View Solution0.18 किग्रा द्रव्यमान के एक गुटके को 2 न्यूटन/मी बल-नियतांक के स्प्रिंग से सलंगन किया है। गुटके और जमीं के बीच घर्षण-गुणांक 0.1है। आरम्भ में गुटका स्थिर है और स्प्रिंग में फैलाव नहीं है। चित्र में दर्शाए अनुसार एक आवेग गुटके को दिया जाता है जिससे गुटका 0.06 मी खिसक कर रुकता है (पहली बार) यदि गुटके का आरम्भिक वेग (मी/से में) v=N10 N का मान होगा
View Solutionऊष्मा के चालक पदार्थ से बने तथा स्थिर रखे गए बेलन की त्रिज्या R तथा ऊँचाई L0 है | बेलन नीचे से खुला है तथा इसके ऊपरी सिरे में एक छोटा छेद है, जैसा कि चित्र में दिखाया गया है | एक पिस्टन जिसका द्रव्यमान M है, ऊपरी सतह से L दुरी पर पकड़ा हुआ है | वायुमण्डलीय दाब P0 है |
अब पिस्टन को बाहर की ओर धीरे - धीरे खिंचा जाता है तथा ऊपर से 2L दूरी पर पकड़ कर रखा जाता है, तब बेलन में ऊपरी सिरे तथा पिस्टन के बीच के भाग में दाब होगा |

View Solutionएक रुक्ष पृथ के उच्चतम बिन्दु से 1 किग्रा द्रव्यमान के गुटके को विरामावस्था से छोडा जाता है। यह पथ 40 मी त्रिज्या का वृत्तीय चाप है। गुटका अपने पथ पर बिना लड़के हुए सरकता है। इस गुटके पर एक घर्षण बल तात्क्षणिक वेग की विपरीत दिशा में लगता है। चित्र में दर्शाए गए अनुसार , बिन्दु O तक आने के लिए घर्षण को अतिक्रम करने के लिए 150 जूल कार्य करना पड़ा है। (गुरुत्वीय त्वरण g=10मी/से2 लीजिए)
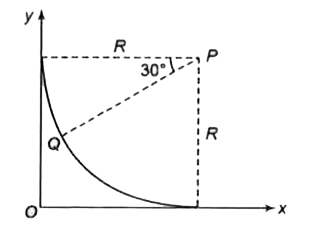 .
.
जब गुटका बिन्दु Q पर पहुँचता है , इसकी गति है
View Solutionलोहे की 0.10 किग्रा की एक गेंद 10 मीटर की ऊँचाई से गिराई जाती है तथा पृथ्वी से टकराकर पुनः 1 मीटर की ऊँचाई तक उछल जाती है मान लीजिए कि गेंद कि यान्त्रिक ऊर्जा का क्षय हुआ अंश पूर्णतः गेंद में ही रह जाता है । गेंद है । गेंद के पदार्थ की विशिष्ट ऊष्मा 0.12 कैलोरी /(ग्राम -°C) है । (i) क्या गेंद को ऊष्मा दी गई ?(ii) क्या गेंद पर कार्य किया गया ? यदि हाँ तो कितना ? (iii) गेंद की आन्तरिक ऊर्जा में क्या परिवर्तन हुआ ? (iv) टकराने पर गेंद के ताप में कितनी वृद्धि हुई ?(g=10 न्यूटन /किग्रा , 4.2J = 1 कैलोरी )
View Solutionएक थैले में 3 सफ़ेद और 6 काली गेंद है तथा दूसरे थैले में 6 सफ़ेद और 3 काली गेंद है यदृच्छयता एक थैले का चयन किया जाता है और उसमे से एक गेंद निकाली जाती है प्रायिकता ज्ञात कीजिए कि निकाली गई सफ़ेद रंग की है।
View Solutionएक थैले में 4 लाल और 3 काली गेंद है दूसरे थैले में 2 लाल व 4 काली गेंद है यादृच्छिक रूप से एक थैले को चुना जाता है तथा उसमे से एक गेंद बाहर निकाली गई , निकाली गई कि लाल होने की प्रायिकता ज्ञात कीजिए
View Solutionदो बॉक्स में क्रमश : 4 सफ़ेद और 2 लाल गेंद तथा 3 सफ़ेद और 7 लाल गेंद है एक बॉक्स को यादृच्छिक रूप से चुना जाता है एवं उसमे से एक गेंद निकाली गई यदि वह गेंद प्रथम बॉक्स से निकाली गई थी
View Solutionतीन थेलो A ,B तथा C में क्रमश : 6 लाल ,4 सफ़ेद ,2 लाल 6 सफ़ेद तथा 1 लाल 5 सफ़ेद गेंद है एक थैले का यादृच्छिक रूप से चयन किया गया तथा उसमे से एक गेंद निकाली जो की लाल रंग की थी प्रायिकता ज्ञात कीजिए की यह गेंद थैला A में से निकाली गई है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionदो अंको की एक संख्या में इकाई स्थान का अंक दहाई स्थान के अंक से 3 अधिक है यदि दोनों अंकों का जोड़ 11 हो तो संख्या निकालिए।
View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?
View SolutionN solid metallic spherical balls are melted and recast into a cylindrical rod whose radius is 3 times that of a spherical ball and height is 4 times the radius of a spherical ball. The value of N is :
N ठोस धात्विक गोलाकार गेंदों को पिघलाकर एक बेलनाकार छड़ बनाया जाता है जिसकी त्रिज्या एक गोलाकार गेंद की त्रिज्या से तिगुनी है और ऊंचाई एक गोलाकार गेंद की त्रिज्या से चोगुनी है |N का मान है :
View Solutionएक काय केंद्रित घनीय जालक का निर्माण B के खोखले गोलों से किया गया है। ठोस A के गोले, B के खोखले गोलों में उपस्थित है। A की त्रिज्या, B की त्रिज्या की आधी है। एकक कोष्ठिका में, A द्वारा अनअधिधारित B के गोलों के कुल आयतन और एकक कोष्ठिका के आयतन का अनुपात क्या है?
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solution
