अपवर्तनांक n1 की एक आयताकार काँच पट्टिका ABCD, अपवर्तनांक n2 के पानी में डुबाई जाती है (n1>n2) | एक प्रकाश किरण पट्टिका के पृष्ठ अब पर आपतित होती है | आपतन कोण का वह अधिकतम मान αmax' जिसके लिए निर्गत किरण दूसरे पृष्ठ CD से बाहर आए, होना चाहिए

sin−1[n1n2cos(sin−1.n2n1)]
sin−1[n1cos(sin−1.1n2)]
sin−1(n1n2)
sin−1(n2n1)
The correct Answer is:A
AB से अपवर्तित होकर आने वाली किरणें AD पर पूर्ण आंतरिक परिवर्तित होकर CD से बाहर आती हैं|
चित्रानुसार, r1+r2=90∘
∴ r1=90∘−r2
(r1)max=90∘−(r2)min तथा (r2)min=θC
जहाँ sinθC=n2n1 या θC=sin−1(n2n1)
∴ (r1)max=90∘−θC
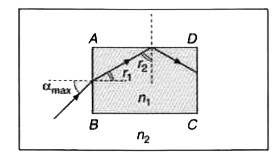
फलक AB पर स्नैल के नियम से,
n1n2=sinαmaxsin(r1)max
=sinαmaxsin(90∘−θC)=sinαmaxcosθC
या sinαmax=n1n2cosθC
∴ αmax=sin−1[n1n2cosθC]
=sin−1[n1n2cossin−1(n2n1)]
Topper's Solved these Questions
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - बहुविकल्पीय प्रश्न - II
13 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - सत्य/असत्य
6 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)
2 Videos
- प्रयोगात्मक भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II
3 Videos
Similar Questions
यंग के द्विक - रेखा छिद्र प्रयोग में व्यतिकरण प्रतिरूप में दीप्त तथा अदीप्त फ़्रिंजों की तीव्रताओं में 9 : 1 का अनुपात है | इसका अर्थ है कि
View Solutionएक लम्बे बेलनाकार प्रकाश स्रोत की अक्ष से r दूरी पर रखे पर्दे पर प्रकाश की तीव्रता, r के व्युत्क्रमानुपाती होती है |
View Solutionचित्र में दिखाई गयी पिचकारी में एक पिस्टन वायु को एक चंचू द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ-काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। ओर फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गयी पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमशः 20 मिमी तथा मिमी है। पात्र का ऊपरी भाग वातावरण में खुला है।

पिस्टन को 5 मिमी/से की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है
View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
View Solutionk के किस मान के लिए रेखाएँ y=(2+√3)x+4 तथा y=kx+6 एक दूसरे से 60∘ के कोण पर झुकी है ?
View Solutionएकवर्णी प्रकाश का एक पुंज (beam of light) काँच की एक प्लेट पर 58^(@ के कोण पर आपतित होता है और परावर्तित किरणपुंज पूरी तरह समतल-ध्रुवित पाया जाता है। काँच का अपवर्तनांक निकालें।
View Solutionप्रकाश का अपवर्तन || काँच की आयताकार स्लैब से अपवर्तन || अपवर्तनांक || कुछ प्रश्न
View Solutionλ का वह मान जिसके लिए द्विघात समीकरण x2+(3−λ)x+2=λ के मूलों के वर्गों के योग का मान न्यूनतम है , है ?
View Solutiona के किस मान के लिये समीकरण
(a2−5a+3)x2+(3a−1)x+2=0 का एक मूल दूसरे मूल का दोगुना होगा
View Solutionप्रकाश का अपवर्तन || काँच की आयताकार स्लैब से अपवर्तन || अपवर्तनांक || कुछ प्रश्न
View Solutionप्रकाश का अपवर्तन|काँच की आयताकार स्लैब से अपवर्तन#!#अपवर्तनांक#!#पूर्ण आन्तरिक परावर्तन
View Solutionएक पुस्तक की मोटाई 2 सेमी है और इसमें 800 पृष्ठ है। एक पृष्ठ की मोटाई मानक रूप में ज्ञात कीजिए।
View Solutionयदि कोई किरण किसी दर्पण पर 30∘ पर आपतित होती है तो परावर्तित कोण का मान होगा
View Solutionएक व्यक्ति पश्चिम दिशा की ओर मूँह करके खड़ा है | वह दक्षिणावर्त दिशा में 45∘ के कोण पर घूमता है फिर वह पुनः उसी दिशा में 180∘ के कोण पर घूमता है और फिर वह वामावर्त दिशा में 270∘ के कोण पर घूमता है | अब वह किस दिशा की ओर खड़ा है ?
View Solutionअभिक्रिया, N2O4⇔2NO2(g) के लिए 1atm पर N2O4 के वियोजन की कोटि 0.2 है, तो 2NO2⇔N2O4 का Kp है:
View Solutionएक निश्चित ताप पर N2O4 का वाष्प घनत्व 30 है। इस ताप पर N2O4 का प्रतिशत वियोजन क्या है?
View Solution
