यंग के द्विछिद्री प्रयोग में प्रयुक्त प्रकाश स्रोत दो तरंगदैर्ध्यों λ1=400nm तथा λ2=600nm को उत्सर्जित करता है | यदि तरंगदैर्ध्यों λ1 तथा λ2 के लिए अभिलिखित फ्रिंज चौड़ाइयाँ क्रमशः β1 तथा β2 हैं, तथा केंद्रीय दीप्त फ्रिंज के एक ओर y दूरी तक फ़्रिंजों की संख्या क्रमशः m1 तथा m2 हैं, तब
β2>β1
m1>m2
केंद्रीय दीप्त फ्रिंज से λ2, की तीसरी दीप्त फ्रिंज, λ1 की पाँचवीं अदीप्त फ्रिंज को ढकती है
λ1 की फ़्रिंजों का कोणीय पृथक्करण λ2 की फ़्रिंजों के कोणीय पृथक्करण से अधिक है
The correct Answer is:A, B, C
प्रिज्म चौड़ाई β=λDd या β∝λ
∴ λ2>λ1
अतः β2>β1
दी गई चौड़ाई में फ्रिंजों की संख्या
m=yβ या mμ1β
⇒ m2<m1 या β2>β1
केंद्रीय दीप्त फ्रिंज से λ2 के तृतीय दीप्त फ्रिंज की दुरी
=3λ2Dd=1800Dd
केंद्रीय दीप्त फ्रिंज से λ1 के पाँचवें अदीप्त फ्रिंज की दुरी
=9λ1D2d=1800Dd
इसलिए λ2 की तृतीय दीप्त फ्रिंज , λ1 की पाँचवी अदीप्त फ्रिंज के साथ अतिव्यापित होगी|
कोणीय दुरी (या कोणीय फ्रिंज चौड़ाई ) =λdμλ
⇒ कोणीय दुरी λ1 के लिए न्यूनतम होगी|
Topper's Solved these Questions
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - सत्य/असत्य
6 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - रिक्त स्थानों की पूर्ति कीजिए
14 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)
2 Videos
- प्रयोगात्मक भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II
3 Videos
Similar Questions
एक लम्बे बेलनाकार प्रकाश स्रोत की अक्ष से r दूरी पर रखे पर्दे पर प्रकाश की तीव्रता, r के व्युत्क्रमानुपाती होती है |
View Solutionएक प्रकाश तरंग जिसकी आवृत्ति 5×1014 हर्ट्ज है 1.5 अपवर्तनांक के एक माध्यम में प्रवेश करती है माध्यम में प्रकाश का वेग ..................................... तथा उसकी तरंगदैर्ध्य ................................ है |
View Solutionचित्र में XY एक पृष्ठ है जो दो पारदर्शी माध्यमों, माध्यम -1 तथा माध्यम -2 को अलग करता है | रेखाएँ ab तथा cd माध्यम -1 में चल रहीं तथा पृष्ठ XY पर आपतित होने वाली प्रकाश - तरंग के तरंग्रागों को निरूपित करती हैं | रेखाएँ ef तथा gh अपवर्तन के बाद माध्यम -2 में चल रही प्रकाश तरंग के तरंग्रागों को निरूपित करती हैं |
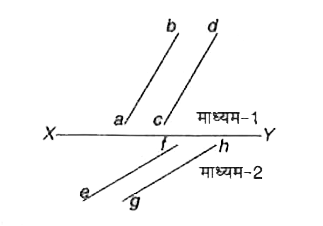
प्रकाश चल रहा ह
View Solutionचित्र में दिखाई गयी पिचकारी में एक पिस्टन वायु को एक चंचू द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ-काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। ओर फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गयी पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमशः 20 मिमी तथा मिमी है। पात्र का ऊपरी भाग वातावरण में खुला है।

पिस्टन को 5 मिमी/से की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है
View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
View Solutionlambda_(1) and lambda_(2) are used to illuminated the slits. beta_(1) and beta_(2) are the corresponding fringe widths. The wavelength lambda_(1) can produce photoelectric effect when incident on a metal But the wavelength lambda_(2) cannot produce photoelectric effect. The correct relation between beta_(1) and beta_(2) is
View Solutionएक प्रोटोन तथा एक फरोतों की दी ब्रॉगली तरंगदैर्ध्य क्रमश: λ1तथाλ2 है। प्रोटोन की गतिज ऊर्जा तथा फोटोन की ऊर्जा (E) सामान है। सिद्ध कीजिएः की λ1λ2α√E
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionदो बिंदुओं P और Q के स्थिति सदिश क्रमशः 2¯a+¯b और ¯a−2¯b है। एक बिंदु R का स्थिति सदिश ज्ञात कीजिए जो रेखा खण्ड PQ को 1:2 के अनुपात में अंतः तथा बाहृातः विभाजित करता है।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
रैखिक प्रोग्रामन समस्या को हल करने के लिए निम्न चरण प्रयुक्त होते हैं -
यदि उच्चतम तथा निम्नतम मान क्रमशः M तथा N हों तथा सुसंगत क्षेत्र प्रतिबंधित (bounded) हो तो M तथा N क्रमश उद्देश्य फलन के उच्चतम तथा निम्नतम मान होते हैं।
View Solutionयदि एक त्रिभुज , जिसका एक शीर्ष परवलय के शीर्ष परवलय y2+4(x−a2)=0 तथा अन्य दोनों शीर्ष y-अक्ष तथा परवलय के प्रतिच्छेदन बिंदुओं पर हैं , का क्षेत्रफल 250 वर्ग इकाई है , तो 'a' का एक मान है
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View Solutionयदि f(x)=Asin(πx2)+B,.f'(12)=√2 तथा ∫10f(x)dx=2Aπ तब A तथा B के मान है
View Solutionयदि a तथा b इकाई सदिश हैं तथा θ इनके बीच का कोण है। तब ∣∣ˆa+ˆb∣∣<1 यदि
View SolutionIf the characteristic wavelengths of the x-rays and the-rays respectively lambda_(1) " तथा " lambda_(2) Then there will be a relationship between them
View Solution
