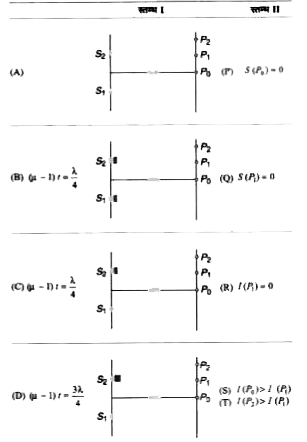
स्तम्भ I में स्टैण्डर्ड यंग द्वि - स्लिट विन्यास की चार परिस्थितयाँ दिखाई गई है | जिनमें स्लिट S1 तथा S2 स्क्रीन से काफी दूरी पर है | प्रत्येक परिस्थिति में S1P0=S2P0,S1P1−S2P1=λ/4 और S1P2−S2P2=λ/3, जहाँ λ प्रकाश की तरंगदैर्ध्य है | B, C व D परिस्थितियों में स्लिट S1 के सामने μ अपवर्तनांक और t मोटाई की पारदर्शी शीट रखी गई है | इन सीटों की मोटाई प्रत्येक परिस्थिति में भिन्न - भिन्न है | स्क्रीन के किसी बिंदु P पर दोनों स्लिट से पहुँच रही प्रकाश तरंगों के फेज - अंतर को S( P ) से निरूपित किया गया है | तथा प्रकाश की तीव्रता को I ( P ) से निरूपित किया गया है | स्तम्भ I की प्रत्येक परिस्थितियों के लिए स्तम्भ II के प्रकथनों को आपस में मिलाइए |
ABCDPQRS,T,P
ABCDT,SQ,PP,RR,T
ABCDQ,P,S,TP,RQ,ST
ABCDP,SQTR,S,T
The correct Answer is:(A)→(P,S),(B)→(Q),(C)→(T),(D)→(R,S,T)
(A) I(P1)=I1+I2+2√I1I2cos.π4
=I0+I0+2I01√2
=(2+√2)I0
I(P0)=I1+I2+2√I1I2cos.2π3
=I0+I0+2I0(−12)=I0
∴ I(P0)>I(P2)
(B) δ(P0)=(μ−1)t2πλ
=λ4.2πλ=π2
δ(P1)=[(μ−1)t−λ4].2πλ=0
δ(P2)=[(μ−1)t−λ/3].2πλ=−π6
I(P0)=I1+I2=2√I1I2cosδ(P0)=2I0
I(P1)=I0
I(P2)=I0+I0+2I0cos(−π6)=(2+√3)I0
(C) δ(P0)=(μ−1)t2πλ=λ2.2πλ=π
δ(P1)=[(μ−1)t−λ4]2πλ=π/2
δ(P2)=[(μ−1)t−λ3].2πλ=π/3
I(P0)=I0+I0+2I0cosπ=0
I(P1)=I0+I0+2I0cos(π/2)=2I0
I(P2)=I0+I0+2I0cos(π3)=3I0
∴ I(P2)>I(P1)
(D) δ(P0)=3λ4.2πλ=3π2
δ(P1)=[(μ−1)t−λ/4]2πλ
=(3λ4−λ4)2πλ=π
δ(P2)=(μ−1)t−λ/3]2πλ=[3λ4−λ3]2πλ=5π6
I(P0)=I0+I0+2I0cos(3π2)=2I0
I(P1)=I0+I0+2I0cos(π)=0
I(P2)=I0+I0+2I0cos(3π6)
=2I0+2I0×−√32=(2−√3)I0
I(P0)>I(P1) तथा I(P2)>I(P1)
Topper's Solved these Questions
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - एकल पूर्णांक उत्तर प्रकार
7 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - विश्लेषणात्मक प्रश्न
40 Videos
- प्रकाशिकीBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रकाशिकीEXERCISE - दृढकथन - कारण प्रकार
1 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)
2 Videos
- प्रयोगात्मक भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रयोगात्मक भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II
3 Videos
Similar Questions
एक पतले उभयोत्तल लेंस की फोकस दूरी 20 सेमी है | जब लेंस के सामने बिम्ब को 25 सेमी से 50 सेमी दूर ले जाया जाता है तो इसके प्रतिबिम्ब का आवर्धन m25 से n50 हो जाता है | m25m50 अनुपात का मान क्या होगा ?
View Solutionकाँच के पतले अवतालोत्तल लेंस (अपवर्तनांक 1.5 ) के उत्तल पृष्ठ की वक्रता त्रिज्या 20 सेमी है | अवतल पृष्ठ की वक्रता त्रिज्या 60 सेमी है | उत्तल पृष्ठ पर चाँदी की कलई की गई है तथा इसे क्षैतिज तल पर रखा जाता है |
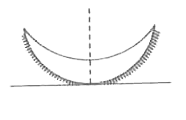
(a) मुख्य अक्ष पर एक पिन कहाँ रखी जाए, जिससे कि उसका प्रतिबिम्ब उसी स्थान पर बन जाए ?
(b) यदि अवतल भाग को जल ( अपवर्तनांक 4/3 ) से भर दिया जाए, तो बताइये पिन को कितना खिसकाना होगा कि पिन का प्रतिबिम्ब फिर पिन पर बने ?
View Solutionकथन I गोलीय दर्पण लिए u, v एवं f के बीच सम्बन्ध स्थापित करने वाला सूत्र केवल उन दर्पणों के लिए सही है जिनके आकार उनकी वक्रता - त्रिज्याओं की तुलना में बहुत छोटे होते हैं |
कथन II प्रकाश के परावर्तन नियम समतल दर्पण लिए तरह सही हैं, परन्तु बड़े आकार की गोलीय सतहों के लिए नहीं |
View Solutionचित्र में दिखाई गयी पिचकारी में एक पिस्टन वायु को एक चंचू द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ-काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। ओर फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गयी पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमशः 20 मिमी तथा मिमी है। पात्र का ऊपरी भाग वातावरण में खुला है।

पिस्टन को 5 मिमी/से की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है
View Solutionएक छात्र ने u-v विधि से अवतल दर्पण की फोकस दूरी निकालने का प्रयोग किया। प्रयोग में उपयोग किये गये अवतल दर्पण की फोकस दूरी 24 cm तथा प्रकाशीय बैच की लम्बाई 1.5 m थी। प्रतिबिम्ब की स्थिति के निर्धारण में हुई अधिकतम त्रुटि 0.2 cm हो सकती है। छात्र द्वारा लिखे गये (u.v) के पांच मान (cm में) इस प्रकार थे. (42.56). (48.48). (60, 40). (66.33). (78.39)। (u.v) के मान जो प्रयोग के द्वारा प्राप्त नही हो सकते और गलत लिखे गये, वह है (वे हैं)
View SolutionLet Sn=1+2+3++n and Pn=S2S2−1⋅S3S3−1⋅S4S4−1⋅⋅⋅SnSn−1 Where n∈N,(n≥2). Then limx→∞Pn=______
View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
The coordinates of P1 are
View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
The ratio area(ΔP1P2P3)area(ΔC1C2C3) is equal to
View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
P2 and P3 are images of each other with respect to the line
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. The co-ordinates of P1 are :
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. The ratio area(ΔP1P2P3)area(ΔC1C2C3) is equal to :
View SolutionLet each of the circles,
S1=x2+y2+4y−1=0,
S2=x2+y2+6x+y+8=0,
S3=x2+y2−4x−4y−37=0
touches the other two. Let P1,P2,P3 be the points of contact of S1andS2,S2andS3,S3andS1 respectively and C1,C2,C3 be the centres of S1,S2,S3 respectively.
Q. P2andP3 are image of each other with respect to line :
View SolutionColumn I shows four situations of standard Young’s double slit arrangement with the screen placed far away from the slits S1 and S2 . In each of these cases S1P0=S2P0,S1P1−S2P1=λ/4 and S1P2−S2P2=λ/3, where λ is the wavelength of the light used. In the cases B,C and D, a transparent sheet of refractive index μ and thickness t is pasted on slit S1 . The thicknesses of the sheets are different in different cases. The phase difference between the light waves reaching a point P on the screen from the two slits is denoted by δ(P) and the intensity by I(P). Match each situation given in Column I with the statement(s) in Column II valid for that situation.
View Solutionα,β,γ are the roots of the cubic equation x3+p1x2+p2x+p3=0. If Sr=αr+βr+γr,S1=10,S2=38 and S3=−1840, then p3=
View Solutionα,β,γ are the roots of the cubic equation x3+p1x2+p2x+p3=0. If Sr=αr+βr+γr,S1=10,S2=38 and S3=−1840, then p3=
View Solution
