
तब f−g है
एकैकी और अन्तःक्षेपी
न तो एकैकी और न आच्छादक
बहुएकैकी और आच्छादक
एकैकी और आच्छादक
The correct Answer is:D
f−g= f(x)−g(x)
={x−0=x;x∈Q0−x=−x;x∈Q'
परिमेय और अपरिमेय संख्या मिलकर वास्तविक संख्या का समुच्चय बनाती है।
एकैकी फलन के लिए हम देखते हें यदि f(x1)=f(x2)⇒x1=x2
परिमेय के लिए
f(x1)−g(x1)=f(x2)−g(x2)
x1=x2
एकैकी फलन है
अपरिमेय के लिए
f(x1)−g(x1)=f(x2)−g(x2)
−x1=−x2
x1=x2
एकैकी फलन है।
परिमेय और अपरिमेय दोनों के लिए एकैकी है
आच्छादक के लिए शर्त : परिसर = सहप्रांत (यहाँ सहप्रांत नहीं दिया है तो हम वास्तविक संख्या के समुच्चय R को ही सहप्रांत मानेंगे )
अब देखिए परिमेय संख्या के लिए हमे मिला f−g=x अर्थात सभी धनात्मक वास्तविक संख्या प्राप्त होंगी
अपरिमेय संख्या के लिए हमे मिला f−g=−x अर्थात सभी ऋणात्मक वास्तविक संख्या प्राप्त होंगी।
अतः परिसर में हमें सभी प्रकार की वास्तविक संख्या (धनात्मक और ऋणात्मक ) मिल गई ।
परिसर =सहप्रांत = R
अतः फलन आच्छादक भी है
अतः f−g एकैकी और आच्छादक दोनों है।
Topper's Solved these Questions
- फलनBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - फलनEXERCISE - बहुविकल्पीय प्रश्न (II)
8 Videos
- फलनBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - फलनEXERCISE - रिक्त स्थानों की पूर्ति कीजिए
6 Videos
- प्रायिकताBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रायिकताEXERCISE - एकल पूर्णांक प्रश्न
2 Videos
- लघुगणक एवं उनके गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - लघुगणक एवं उनके गुणEXERCISE - एकल पूर्णांक प्रश्न
1 Videos
Similar Questions
यदि y=f(x)=x+2x−1, तब
View Solutionf(x)=3sin(√π216−x)का मान अन्तराल .............. में है।
View Solutionतीन स्वतंत्र घटनाओं E1,E2 तथा E3 में से केवल E1 के घटने की प्रायिकता α है केवल E2 के घटने की प्रायिकता β है तथा केवल E3 के घटने की प्रायिकता γ है। माना कि घटनाओं E1,E2 या E3 में से किसी के भी न घटने की प्रायिकता p, समीकरणों (α−2β)p=αβ तथा (β−3γ)p=2βγ को संतुष्ट करती है। सभी प्रायिकताएं अंतराल (0,1) में स्थित मानी जाती है तब E1के घटने की प्रायिकताE3के घटने की प्रायिकता=
View Solutionपद 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2…………..⎞⎟ ⎟⎠ का मान है
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
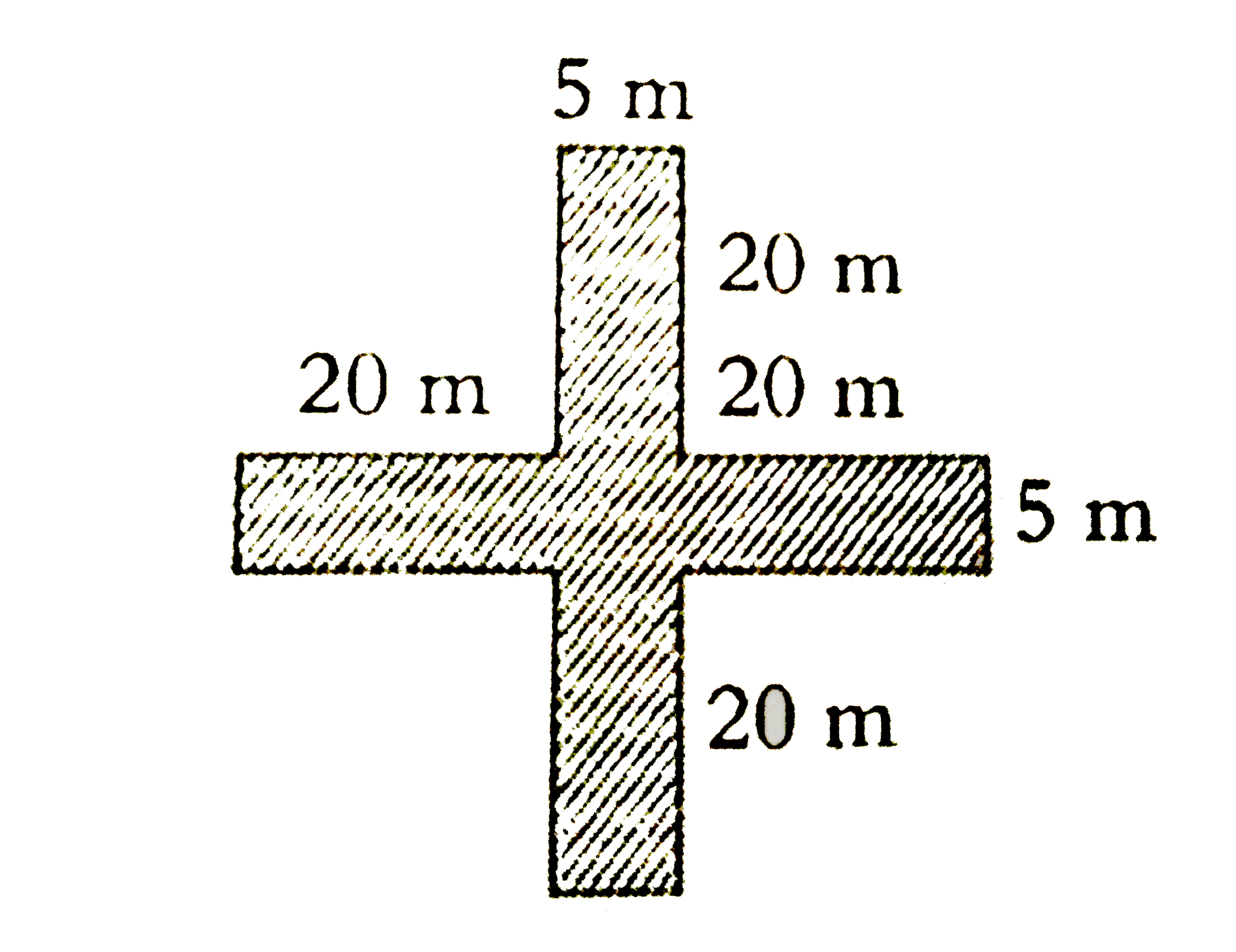
View SolutionThe area of the shaded part in the figure given below is ______.
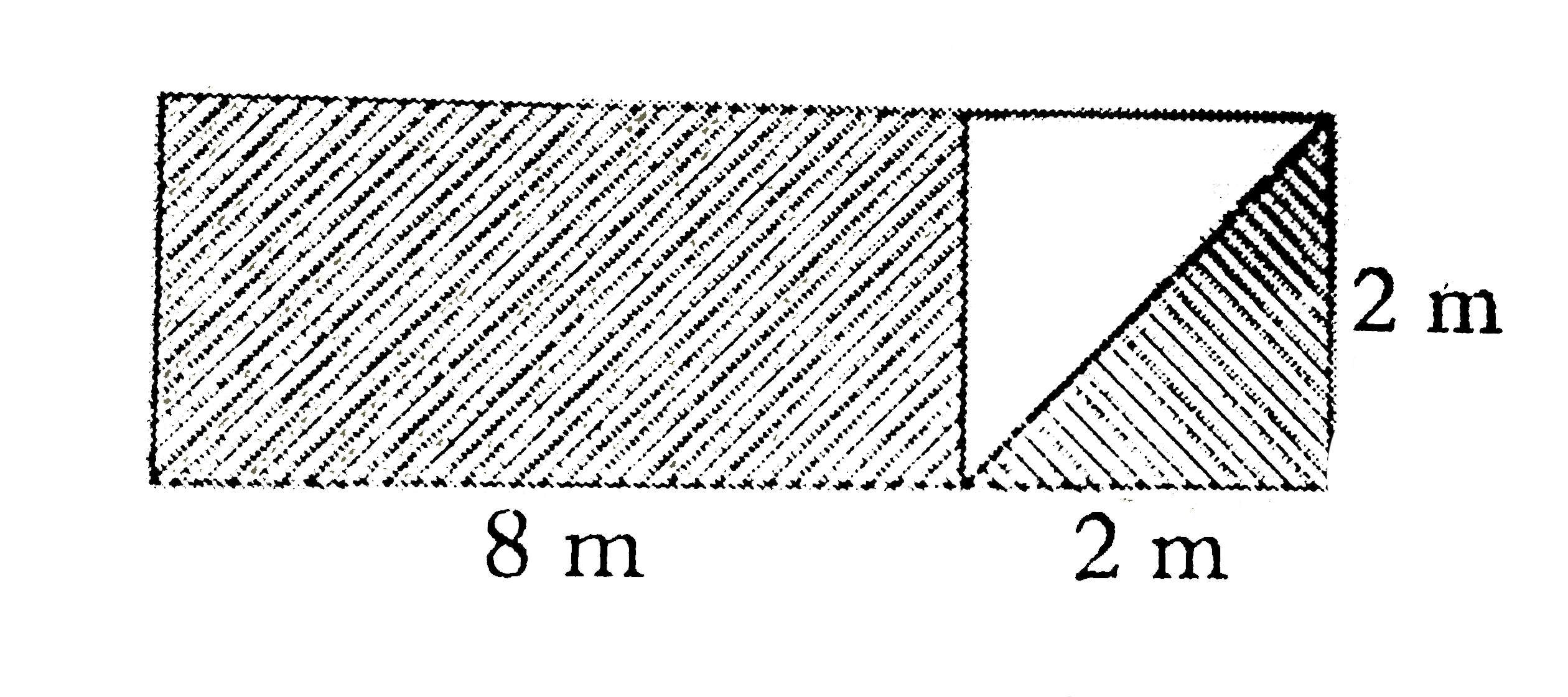
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solution
