माना सभी वास्तविक x के लिए f(x)=2+cosx
कथन - 1 : सभी वास्तविक t के लिए [t,t+π] में एक बिन्दु इस प्रकार है कि f'(c)=0 क्योंकि
कथन - 2 : f(t)=f(t+2π) प्रत्येक वास्तविक t के लिए
The correct Answer is:(b)
Step by step video, text & image solution for माना सभी वास्तविक x के लिए f(x) = 2 + cos x कथन - 1 : सभी वास्तविक t के लिए [t, t + pi] में एक बिन्दु इस प्रकार है कि f'(c) = 0 क्योंकि कथन - 2 : f(t) = f( t+ 2pi) प्रत्येक वास्तविक t के लिए by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- फलनBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - फलनEXERCISE - विश्लेषणात्मक प्रश्न
7 Videos
- फलनBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - फलनEXERCISE - मैट्रिक्स-सुमेल प्रकार
2 Videos
- प्रायिकताBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - प्रायिकताEXERCISE - एकल पूर्णांक प्रश्न
2 Videos
- लघुगणक एवं उनके गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - लघुगणक एवं उनके गुणEXERCISE - एकल पूर्णांक प्रश्न
1 Videos
Similar Questions
माना y=√(x+1)x−3x−2,x के वे सभी वास्तविक मान ज्ञात कीजिए। जिनके लिए y का मान वास्तविक है।
View Solutionमाना स्तम्भ I में परिभाषित फलन का प्रान्त (−π2,π2) एक तथा परास (−∞,∞) है
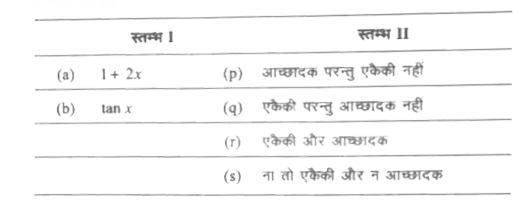
View Solutionतीन स्वतंत्र घटनाओं E1,E2 तथा E3 में से केवल E1 के घटने की प्रायिकता α है केवल E2 के घटने की प्रायिकता β है तथा केवल E3 के घटने की प्रायिकता γ है। माना कि घटनाओं E1,E2 या E3 में से किसी के भी न घटने की प्रायिकता p, समीकरणों (α−2β)p=αβ तथा (β−3γ)p=2βγ को संतुष्ट करती है। सभी प्रायिकताएं अंतराल (0,1) में स्थित मानी जाती है तब E1के घटने की प्रायिकताE3के घटने की प्रायिकता=
View Solutionपद 6+log32⎛⎜ ⎜⎝13√2 ⎷4−13√2 ⎷4−13√2√4−13√2…………..⎞⎟ ⎟⎠ का मान है
View Solutionlet f(x)=2+cos x for all real x Statement 1: For each real t,there exists a pointc in [t,t+pi] such that f'(c)=0 Because statement 2:f(t)=f(t+2 pi) for each real t
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionवास्तविक संख्याओं के लिए घातांक नियम || उदाहरण
View Solutionवास्तविक संख्या x के लिए संतुष्ट के लिए, x2−|x+2|+x>0 होगा?
View Solutionएक द्विघात बहुपद f(x), जो f(0)=0,f(1)=1,f'(x)>0, को सभी x∈(0,1) के लिए संतुष्ट करता है, है
View Solutionमाना f(x)={x0<x≤2 के लिए1x=0 के लिए ' है, तो x = 0 पर फलन का
View Solutionमाना की f:R→R इस प्रकार का अवकलनीय फलन (differentiable function) है की f(0),0,f(π2)=3 एव f'(0)=1 है|
यदि x∈(0,π2] के लिए g(x)=∫x2x[f'(t) cosec t-cot t cosec f(t) dt ]हैतबlimx→0g(x)=
View Solutionदिया है बहुपद f(x)=1+2x+3x2+4x3.
माना कि f(x) के भिन्न, वास्तविक मूलो का योग S है तथा t=|S| है |
Q. वास्तविक संख्या S, निम्न अन्तराल में है
View Solutiona का वह मान जिसके लिए फलन f(x)=√3sinx−cosx−2ax+b सभी x के लिए ह्रासमान है, होगा
View Solutionएक फलन g जो प्रत्येक वास्तविक संख्या x>0 के लिए परिभाषित है तथा g(1)=1,g'(x2)=x3 को सभी x>0 के लिए सन्तुष्ट करता है, तो g (4) का मान है
View Solutionउपयुक्त प्रतिबंध लगाकार निम्नलिखित कथनो को पुनः इस प्रकार लिखिए की वे सत्य कथन हो जाएँ।
प्रत्येक वास्तविक संख्या x के लिए 2x>x होगा।
View Solutionउपयुक्त प्रतिबंध लगाकार निम्नलिखित कथनो को पुनः इस प्रकार लिखिए की वे सत्य कथन हो जाएँ।
प्रत्येक वास्तविक संख्या x के लिए x2≥x होगा।
View Solution
