माना Sn=n∑k=1nn2+kn+k2 एवं Tn=n∑k=0nn2+kn+k2 , n = 1, ,2, 3 ....... के लिए , तब
Sn<π3√3
Sn>π3√3
Tn<π3√3
Tn>π3√3
The correct Answer is:A, B
Step by step video, text & image solution for माना S_(n)= sum_(k=1)^(n)(n)/(n^(2)+kn+k^(2)) एवं T_(n) = sum_(k=0)^(n) (n)/(n^(2)+kn+k^2) , n = 1, ,2, 3 ....... के लिए , तब by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- निश्चित समाकलन BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - निश्चित समाकलन EXERCISE - रिक्त स्थानों की पूर्ति कीजिए
9 Videos
- निश्चित समाकलन BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - निश्चित समाकलन EXERCISE - मैट्रिक्स-सुमेल प्रकार
1 Videos
- निश्चित समाकलन BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - निश्चित समाकलन EXERCISE - एकल पूर्णाक प्रश्न
7 Videos
- द्विपद प्रमेयBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - द्विपद प्रमेयEXERCISE - एकल पूर्णांक प्रश्न
3 Videos
- परवलयBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - परवलयEXERCISE - एकल पूर्णांक प्रश्न
5 Videos
Similar Questions
f(x)=∣∣ ∣ ∣∣secxcosxsec2x+cotxcosecxcos2xcos2xcosec2x1cos2xcos2x∣∣ ∣ ∣∣ तो ∫π/20f(x)dx=..........
View Solutionस्तम्भ I में दिए गए समाकलनो का स्तम्भ II में दिए गए मानो के साथ सुमेल कराये।
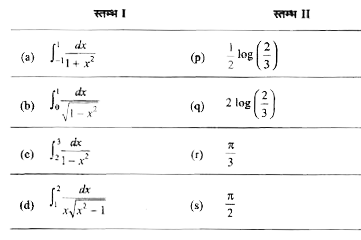
View Solutionदिया है कि किसी वास्तविक संख्या x के लिए [x], अधिकतम पूर्णांक को दर्शाता है यदि अन्तराल [−10,10] पर वास्तविक मानों वाला फलन f निम्न प्रकार से परिभाषित है f(x)={x−[x],if [x] is Odd,1+[x]−x, if [x] is Even तो π210∫10−10f(x)cosπxdx का मान है
View Solution(1+x)n+5 के तीन क्रमागत पदों के गुणांक 5 : 10 : 14 के अनुपात में है, तब n का मान ज्ञात कीजिए ।
View Solutiony2=8x एक परवलय है। मान लीजिए एक त्रिभुज का क्षेत्रफल है जो नाभिलम्ब जीवा के सिरों और परवलय के बिन्दु P(12,2) द्वारा निर्मित है और Δ2 उस त्रिभुज का क्षेत्रफल है, जो बिन्दु P पर और नाभिलम्ब जीवा के सिरों पर खींची गई स्पर्शियों द्वारा बना है। तब Δ1Δ2 है।
View Solutionprove that sum_(k=1)^(n)k2^(-k)=2[1-2^(-n)-n*2^(-(n+1)))
View SolutionS_(n)=sum_(k=1)^(n)(k^(2)+n^(2))/(n^(3)) and T_(n)=sum_(k=0)^(n-1)(k^(2)+n^(2))/(n^(3)),n in N then
View SolutionIf n∈N,n∑k=1sin−1(xk)=nπ2t h e nn∑k=1xk
View SolutionLet U_(n)=sum_(k=1)^(n)(n)/(n^(2)+k^(2)),S_(n)=sum_(k=0)^(n-1)(n)/(n^(2)+k^(2)) then
View SolutionIf sum_(n=1)^(5)(1)/(n(n+1)(n+2)(n+3))=(k)/(3), then k is equal to :-
View SolutionLet a_(n)=sum_(k=1)^(n)(1)/(k(n+1-k)), then for n>=2
View SolutionGiven S_(n)=sum_(k=1)^(n)(k)/((2n-2k+1)(2n-k+1)) and T_(n)=sum_(k=1)^(n)(1)/(k) then (T_(n))/(S_(n)) is equal to
View SolutionIf sum_(k=1)^n(sum_(m=1)^k m^2)=a n^4+b n^3+c n^2+dn+e then -
View SolutionLet lim_(n rarr oo)(((kn)!)/(n^(kn)))^(1/n)=lambda(k) where k in N
View SolutionEvaluate :
(i) 10∑n=1(2+3n) (ii) n∑k=1[2k+3(k−1)] (iii) 8∑n=15n
View Solution
