If a=3+i and z=2−3i then the points az, 3az and −az are: Solution in Tamil
vertices of a right angled triangle
vertices of an equilateral triangle
vertices of an isosceles triangle
collinear
The correct Answer is:D
Step by step video, text & image solution for If a=3+i and z=2-3i then the points az, 3az and -az are: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - PREMIERS PUBLISHERSCHAPTER - COMPLEX NUMBERSEXERCISE - Solution to Exercise 2.9
25 Videos
- APPLICATIONS OF VECTOR ALGEBRABOOK - PREMIERS PUBLISHERSCHAPTER - APPLICATIONS OF VECTOR ALGEBRAEXERCISE - PROBLEMS FOR PRACTICE (Answer the following questions)
21 Videos
- DIFFERENTIALS AND PARTIAL DERIVATIVESBOOK - PREMIERS PUBLISHERSCHAPTER - DIFFERENTIALS AND PARTIAL DERIVATIVESEXERCISE - PROBLEMS FOR PRACTICE
40 Videos
Similar Questions
in+in+1+in+2+in+3
View SolutionProve that the sum of the squares of the squares of tha diagonals of a parallelogram is equal to tha sum of the squares of its sides.
(## CTN_MK_MAT_X_P2_GEO_CO2_E11_001.png" width="80%">
View SolutionThe percentage error of the seventh root of 700 is approximate how many times the percentage of 700:
View SolutionIf the polynomials az^(3)+4z^(2)+3z-4 and z^(3)-4z+a leave the same remainder when divided by z-3, find the value of a.
View SolutionIf one root of the equation z2−az+a−1=0is(1+i),wherea is a complex number then find the root.
View SolutionThe value of 'a' for which the equations 3x-y+az=1,2x+y+z=2,x+2y-az=-1 fail to have unique solution is
View SolutionLet 'z' be a complex number and 'a' be a real parameter such that z2+az+a2=0, then
View SolutionIf roots of the equation z2+az+b=0 are purely imaginary then
View SolutionIf a is a positive integer,z=a+2i and z|z|-az+1=0 then
View SolutionLet 'z' be a comlex number and 'a' be a real parameter such that z2+az+a2=0, then which is of the following is not true ?
View SolutionConsider the equation az+¯¯¯¯bz+c=0, where a,b,c ∈Z
If |a|=|b|≠0andaz+b¯c+c=0 represents
View SolutionFor a complex number Z, if all the roots of the equation Z3+aZ2+bZ+c=0 are unimodular, then
View SolutionIf a>0andz|z|+az+3i=0, then z is
View SolutionLet 'z' be a comlex number and 'a' be a real parameter such that z2+az+a2=0, then which is of the following is not true ?
View SolutionIn the given figure, point A is on the bisector of ∠XYZ.
If AX = 2 cm, then find AZ.
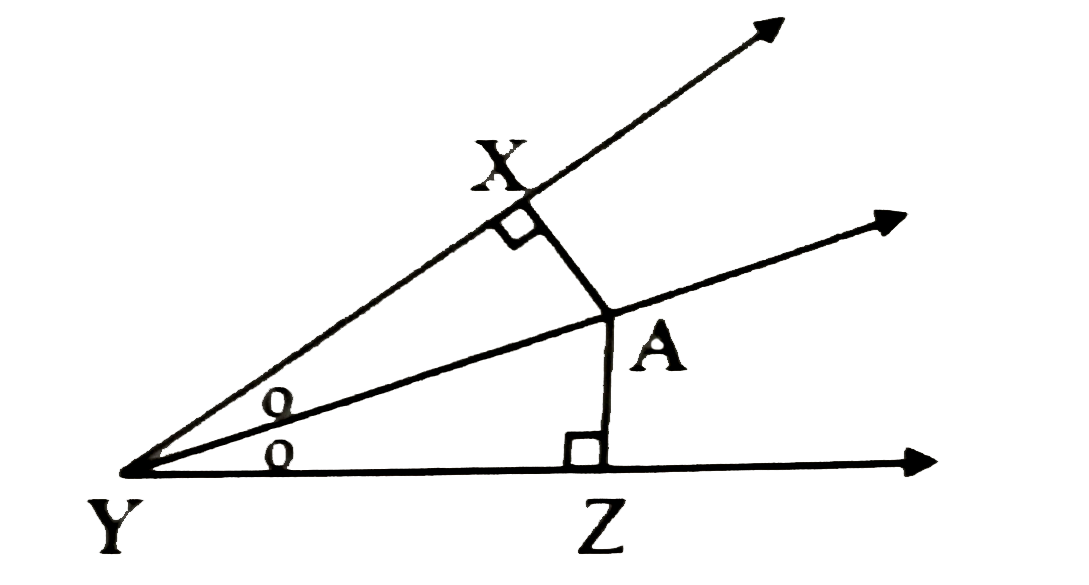
View Solution
