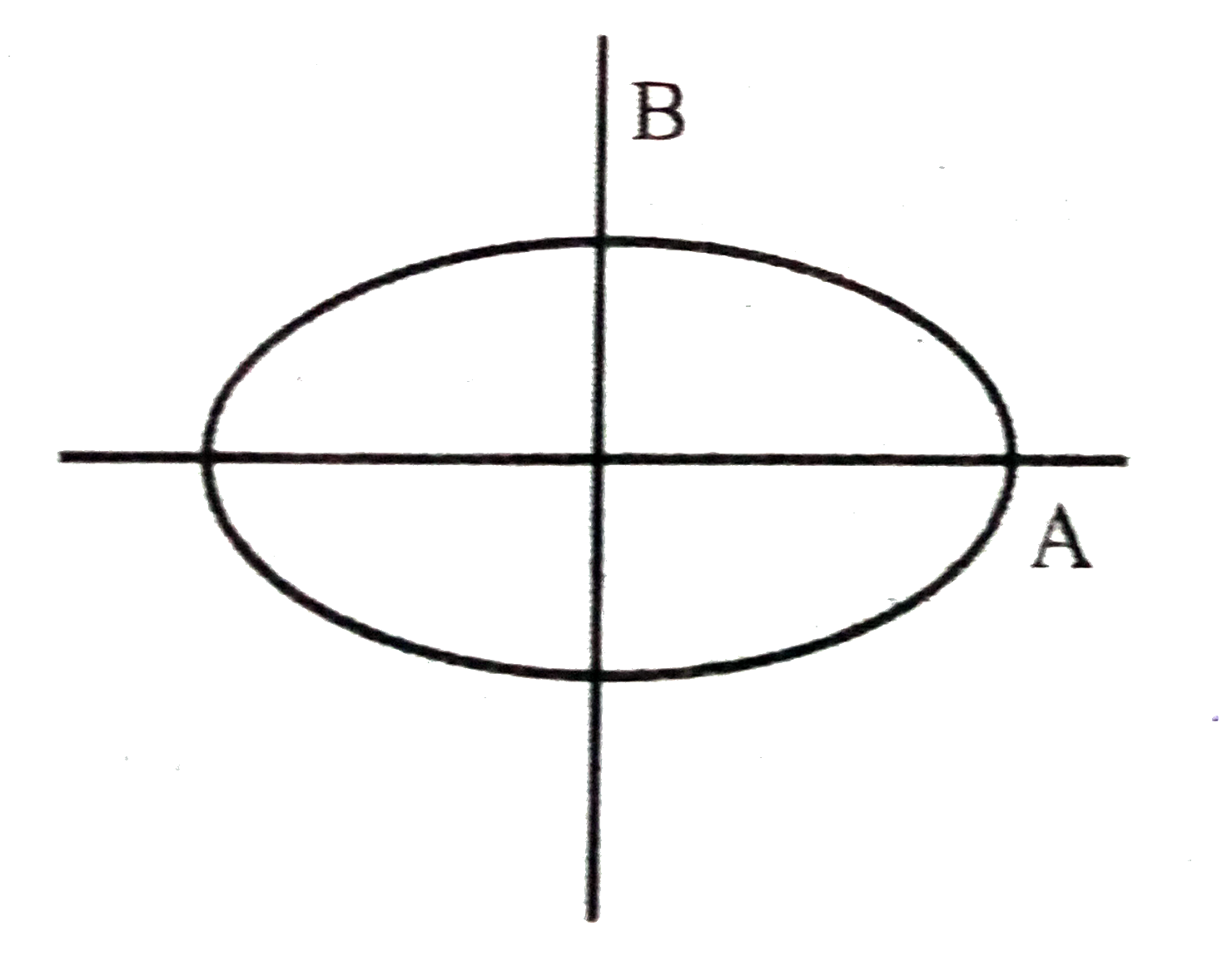
The ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 has the points A and B a

A circle is drawn with the two foci of an ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ at the end of diameter. What is the equation of the circle?
A $x^{2} + y^{2} - a^{2} + b^{2}$
B $x^{2} + y^{2} = a^{2} - b^{2}$
C $x^{2} + y^{2} = 2 (a^{2} + b^{2})$
D $x^{2} + y^{2} = 2 (a^{2} - b^{2})$
The tangents and normal at a point on $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ cut the y-axis A and B. Then the circle on AB as diameter passes through
Aone of the vertex of the hyperbola
Bone of the foot of directrix on x-axis of the hyperbola
Cfoci of the hyperbola
Dnone of these

The ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ has the points A and B as shown here. Find the equation of the circle on AB as diameter.