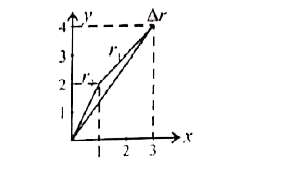
A particle has its position moved from →r1=3ˆi+4ˆj to →r2=ˆi+2ˆj. Calculate the displacment vector (Δ→r) and draw the →r1,→r2andΔ→r vector in a two dimensional Cartesian coordinate system.Solution in Tamil
Given: r1=3i+4j
r2=i+2j
Δr=?
Formula: Δr=r2−r1
=(i+2j)−(3i+4j)
=(1−3)ˆi+(2−4)ˆj
=−2ˆi−2ˆj
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (I.Multiple choice questions).236videos
KINEMATICS
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (II. Very short answer questions).112videos
KINEMATICS
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Textbook questions & answers (III. Long answer questions).16videos
KINEMATICS
- BOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (CONCEPTUAL QUESTIONS)34videos
GRAVITATION
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINETIC THEORY OF GASESEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (VI. Conceptual Questions.)8videos
KINETIC THEORY OF GASES
Similar Questions
Kinematics is the branch of mechanics which delas with the motion of objects without taking _________ into account
03:40View SolutionWhat is Kinematics?
04:13View SolutionIf →A=8ˆi+6ˆj and →B=4ˆi+2ˆj. Then find ∣∣→A+→B∣∣
02:26View SolutionWhy a body weighs less at the equator than at the poles?
04:46View SolutionWhen an automobile travels for a long distance , the air pressure in the tyres increases slightly . Why ?
04:04View SolutionIf →r1,→r2,→r3 are the position vectors of the collinear points and scalar pandq exist such that →r3=p→r1+q→r2, then show that p+q=1.
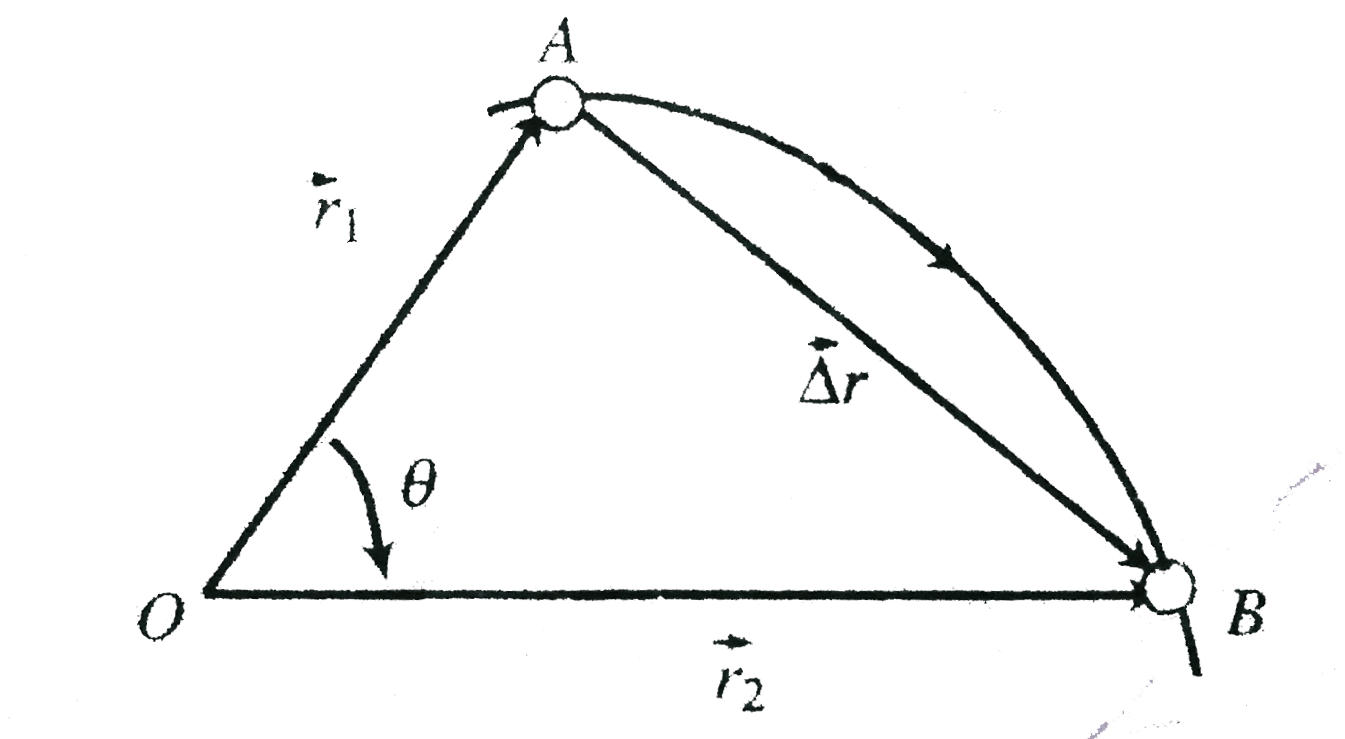
04:25View SolutionA particle moves from position A to position B in a path as shown in If the poit vectors →r1 and →r2 making an angle θ between them are give, find the magnitude of displacement.
. 03:26View SolutionThe resultant of →A+→Bis→R1. On reversing the vector →B, the resultant becomes →R2. What is the value of R21+R22?
02:49View SolutionTwo particles A and B, move with constant velocities →v1 and →v2. At the initial moment their position vectors are →r1 and →r2 respectively. The condition for particle A and B for their collision is
02:08View SolutionA force →F=4ˆi−5ˆj+3ˆk is acting a point →r1=ˆi+2ˆj+3ˆk. The torque acting about a point →r2=3ˆi−2ˆj−3ˆk is
03:14View SolutionA particle has its position moved from vec(r_(1))=3hati+4hatj to vec(r_(2))=hati+2hatj . Calculate the displacment vector (Delta vecr) and draw the vec(r_(1)), vec(r_(2)) and Delta vecr vector in a two dimensional Cartesian coordinate system.
07:28View SolutionCalculate the average velocity of the particle whose position vector changes from →r1=5ˆi+6ˆj to →r2=2ˆi+3ˆj in a tine 5 second.
04:33View Solutionनियत बल →F=5ˆi+5ˆj के अधीन एक कण बिंदु →r1=2ˆi+3ˆj →r2=3ˆi+2ˆj से तक गति करता है । बल द्वारा किये गये कार्य की गणना कीजिए ।
05:13View SolutionA force acting on a body displaces it from position vector →r1=(2ˆi−ˆj+3ˆk)m to →r2=(5ˆi−2ˆj+4ˆk)m. Then find the displacement vector.
04:16View SolutionIf vec(r_(1)) and vec(r_(2)) are the position vectors of mass bodies M_(1) and M_(2) then represent force between them in a vector from.
View Solutionनिम्न रेखाओं के मध्य न्यूनतम दूरी ज्ञात कीजिए
→r1=(ˆi+2ˆj+3ˆk)+λ(2ˆi+3ˆj+4ˆk) तथा →r2=(2ˆi+4ˆj+5ˆk)+μ(3ˆi+4ˆj+5ˆk)01:21View Solution