A particle moves in a circle of radius 4. 0 cm clockwise at constant speed of 2cms−1 , If ˆxandˆy are unit acceleration vectors along x-axis and y-axis respectively (in cms−2) , find the acceleration of the particle at the instant half way between P and Q . Solution in Tamil
Step by step video, text & image solution for A particle moves in a circle of radius 4. 0 cm clockwise at constant speed of 2 cms^(-1) , If hat(x) and hat(y) are unit acceleration vectors along x-axis and y-axis respectively (in cms^(-2)) , find the acceleration of the particle at the instant half way between P and Q . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (IV. Long answer questions).34videos
KINEMATICS
- BOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (CONCEPTUAL QUESTIONS)34videos
GRAVITATION
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINETIC THEORY OF GASESEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (VI. Conceptual Questions.)8videos
KINETIC THEORY OF GASES
Similar Questions
Define and illustrate the following terms.
Equal vectors.07:15View SolutionWhy a body weighs less at the equator than at the poles?
00:57View SolutionWhen an automobile travels for a long distance , the air pressure in the tyres increases slightly . Why ?
01:25View SolutionA particle starts from the origin at t= 0 with a velocity of 8.0 hat j m//s and moves in the x-y plane with a constant acceleration of (4.0 hat i + 2.0 hat j) m//s^2. At the instant the particle's x-coordinate is 29 m, what are (a) its y-coordinate and (b) its speed ?
02:41View Solutionvec(P)+vec(Q) is a unit vector along x-axis. If vec(P)= hat(i)-hat(j)+hat(k) , then what is vec(Q) ?
04:12View SolutionAssertion: If hat(i) and hat(j) are unit Vectors along x-axis and y-axis respectively, the magnitude of Vector hat(i)+hat(j) will be sqrt(2) Reason: Unit vectors are used to indicate a direction only.
04:57View SolutionA particle moves in a circle of radius 4.0cm clockwese at constant speed of 2cmS−1 . If ˆx and ˆy ar unit accleration vectors along X- asis and Y-axis respectively, find the accleration of the particle at the instant half way between PQ. Fig. 2 ( d) . 38.
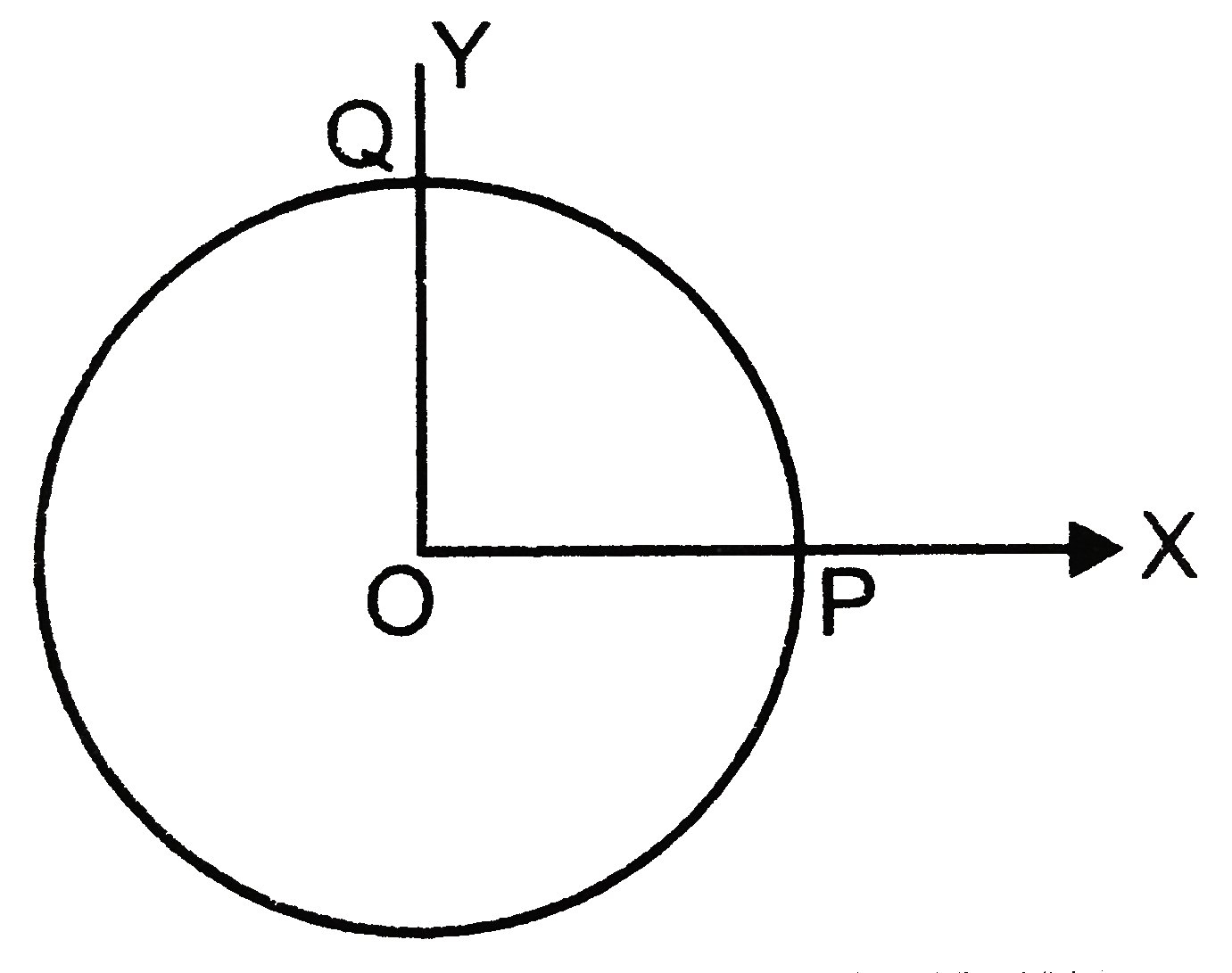.07:34View SolutionThe position vector of a particle moving in x-y plane is given by vec(r)=(t^(2)-4)hat(i)+(t-4)hat(j) . Find (a) Equation of trajectory of the particle (b)Time when it crosses x-axis and y-axis
02:19View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
02:41View SolutionA particle moves in a circle of radius 4.0 cm clockwise at constant speed of 2 ms^(-1) . If hat(x) and hat(y) are unit acceleration vectors along X-axis and Y-axis respectively (in cms^(-2) ), find the acceleration of the particle at the instant half way between P and Q. Refer to Fig.5.14 (a).
03:56View SolutionThe velocity and acceleration vectors of a particle undergoing circular motion are v=2ˆim/sanda=2ˆi+4ˆjm/s2 respectively at some instant of time. The radius of the circle is
03:57View SolutionIf ˆi,ˆjandˆk are unit vectors along x,y and z-axis respectively, the angle θ between the vector ˆi+ˆj+ˆk and vectorˆj is given by
03:50View Solutionयदि ˆi,ˆj,ˆk क्रमशः X-अक्ष Y- अक्ष और Z-अक्ष के अनुदिश इकाई सदिश है , तो ˆi×(ˆj׈k) का मान होगा -
02:09View SolutionA particle moves in a circle of radius 4. 0 cm clockwise at constant speed of 2cms−1 , If ˆxandˆy are unit acceleration vectors along x-axis and y-axis respectively (in cms−2) , find the acceleration of the particle at the instant half way between P and Q .
02:57View SolutionA particle is moving in a clockwise direction with a fixed speed of 2 cm / s on a circle of radius 4 cm. If the acceleration vector in the x and y direction respectively hatx and haty If the particle's acceleration is at the midpoint between P and Q.
02:54View Solution