Explain why a cyclist bends while negotiating a curve road? Solution in Tamil
Let us consider a cyclist negotiating a circular level road (not bankde) of radius r with a speed v. The cycle and the cylcist are considered as one system with mass m. The centre of gravity of the system is C and it goes in a circle of radius r with centre at O. Let us choose the line OC as X-axis and the vertical line through O as Z-axis as shown in the figure.
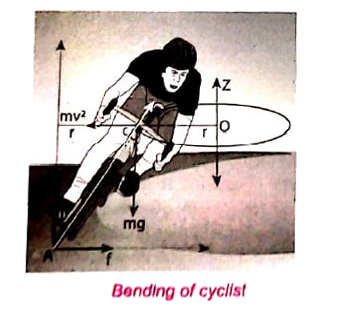
the system as a frame is rotating about z-axis. The system is at rest in this rotating frame. The forces acting on the system are, (i) gravitational force (mg), (ii) normal force (N),(ii) frictional force (f) and (iv) centrifugal force (mv2r). As the system is in equilibrium in the rotaional frame of reference, the net external force and net external torque must be zero. Let us consider all torques about the point A in th figure.
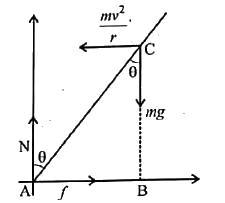
Conditions for rotational equilibrium are
ve(τ)net=0
(i) The torque due to the gravitational force about point a is (mg AB) which causes a clockwise turn that is taken as negative.
(ii) The torque due to the centripetal force is (mv2rBC) which causes an anticlockwise turn that is taken as positive.
−mgAB+mv2rBC=0
mgAB=mv2rBC
From ΔABC,
AB=ACsinθ and BC=ACcosθ
mgACsinθ=mv2rACcosθ
tanθ=v2rg
tanθ=v2rg
θ=tan−1(v2rg)
While negotiating a circular level road of radius r at velocity, v a cyclist has to bend by an angle θ from vertical θ=tan−1(v2rg) to stay in equilibrium (i.e, to avoid a fall). So the cyclist bends while negotiating a curve road.
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND BODIESBOOK - PREMIERS PUBLISHERSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND BODIESEXERCISE - TEXTBOOK QUESTIONS & ANSWERS (CONCEPTUAL QUESTIONS)
16 Videos
- MOTION OF SYSTEM OF PARTICLES AND BODIESBOOK - PREMIERS PUBLISHERSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND BODIESEXERCISE - TEXTBOOK QUESTIONS & ANSWERS (NUMERICAL PROBLEMS)
12 Videos
- MOTION OF SYSTEM OF PARTICLES AND BODIESBOOK - PREMIERS PUBLISHERSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND BODIESEXERCISE - TEXTBOOK QUESTIONS & ANSWERS (SHORT ANSWER QUESTIONS)
34 Videos
- LAW OF MOTION BOOK - PREMIERS PUBLISHERSCHAPTER - LAW OF MOTION EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (VI Numerical Problems)
62 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBOOK - PREMIERS PUBLISHERSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (III. Short Answer Questions.)
24 Videos
Similar Questions
When a tree is cut, the cut is made on the side facing the direction in which the tree is required to fall. Why?
View SolutionA uniform disc of mass 100 g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along a horizontal table with a velocity of 20 cm s−1. (take the surface of table as reference).
View SolutionDefine the center of mass of a body.
View SolutionA scooterist moving with a speed of 36mkmh−1 sees a child standing in the middle of the raod he applies the brakes and brings the scooter to rest in 5s just in time to saved child calculate the average retarding force on the vehicle if mass of the vehicle and drive is 300 kg
View SolutionWhat is meant by Parallax?
View SolutionStatement - I : A cyclist always bends in wards while negotiating a curve.
Statement - II : By bending, he lowers his centre of gravity
View SolutionThe passenger in car are thrown outwards when the car negotiates a curve, but the cyclist bends inwards, while negotiating the same curve. .Then this happens due to
View Solutionवृत्तीय सड़क पर साइकिल सवार, मोड़ के केंद्र की ओर झुकता है क्यों? गणितीय व्याख्या कीजिए।
View SolutionExplain why a cyclist bends while negotiating a curve road?
View SolutionExplain why a cyclist bends while negotiating a curve road?
View SolutionExplain why a cyclist bends while negotiating a curve road?
View SolutionWhile negotiating a circular level road a cyclist has to bend by an angle from vertical to stay in an equilibrium is
View SolutionExplain why a cyclist bends while negotiating a curve road?
View Solution(A) : A cyclist always bends inwards while negotiating a horizontal curve.
(r) : By bending, cyclist lowers his centre of gravity.
View Solution(A) : A cyclicst always bends inwards while negotiating a horizontal curve. (R ) : By bending, cyclist lowers his centre of gravity.
View Solution
