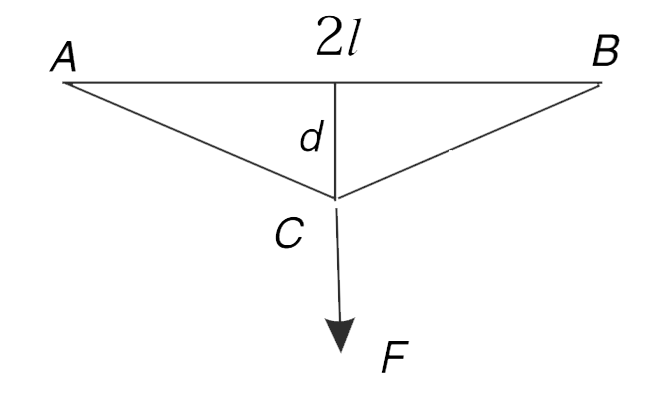
A wire of radius r stretched without tension along a straight line is tightly fixed at A and B. What is the tension in the wire when it is pulled in the shape ACB? Assume Young's modulus of material of the wire to be Y.

Text Solution

Verified by Experts

Let 2l be the original length of wire AB, i.e., L = 2l, when wire is pulled into shape ACB, the increase in length,
$Δ L = (A C + C B) - A B$
$= 2 {(l^{2} + d^{2})}^{1 / 2} - 2 l$
longitudinal strain $= \frac{Δ L}{L}$
$= \frac{2 {(l^{2} + d^{2})}^{1 / 2} - 2 l}{2 l}$
$= \frac{2 l [1 + {(\frac{d^{2}}{l^{2}})}^{1 / 2} - 1]}{2 l}$
$= [1 + \frac{1}{2} \frac{d^{2}}{l^{2}} - 1] = \frac{d^{2}}{2 l^{2}}$
longitudinal stress $= \frac{tension}{area} = \frac{F}{π r^{2}}$
$∴$ Young's modulus,
$Y = \frac{longitudinal stress}{longitudinal strain}$
$\frac{F / π r^{2}}{d^{2} / 2 l^{2}}$
$∴$ Tension in the wire
$F = Y \times π r^{2} \times \frac{d^{2}}{2 l^{2}}$

A uniform wire of density $ρ$ is stretched by $l_{!}$ under its propotional limit whose original slength is L. What is lowest frequency of transverse viberation set up in the wire assuming Young's modulus of the material to be Y?
A $\frac{1}{2 L} \sqrt{\frac{Y l_{1}}{ρ L}}$
B $\frac{1}{4 L} \sqrt{\frac{Y l}{ρ L_{1}}}$
C $\frac{1}{2 L} \sqrt{\frac{Y l_{1}}{ρ L_{1}}}$
D $\frac{1}{L} \sqrt{\frac{Y l_{1}}{ρ L}}$
When a wire is stretched by a force the strain produced in the wire is $2 \times 10^{- 4}$ . If the energy stored per unit volume of the wire is $4 \times 10^{4} joule / m^{3}$ then the Young's modulus of the material of the wire will be,
A $1 \times 10^{12} N / m^{2}$
B $1.5 \times 10^{12} N / m^{2}$
C $2 \times 10^{12} N / m^{2}$
D $2.5 \times 10^{12} N / m^{2}$
A steel wire is stretched with a definite load. If the Young's modulus of the wire is Y. For decreasing the value of Y.
Aradius should be increased
Bradius should be decreased
Clength should be increased
Dnone