How will you determine the velocity of sound using resonance air column apparatus ?

Text Solution

Verified by Experts

The resonance air column apparatus is use to measure the speed of sound in air at room temperature.
Construction:
(i) It consists of a cylinderal galss tube of one meter length whose one end A is open and another end B is connected to the water reservoir R through a rubber tube as shown in Figure.
(ii) This cylinderal galss tube is mounted on a vertiacal stand with a scale attached to it. the tube is partially filled with water and the water level can be adjusted by rasinig lowering the water in the reservior R.
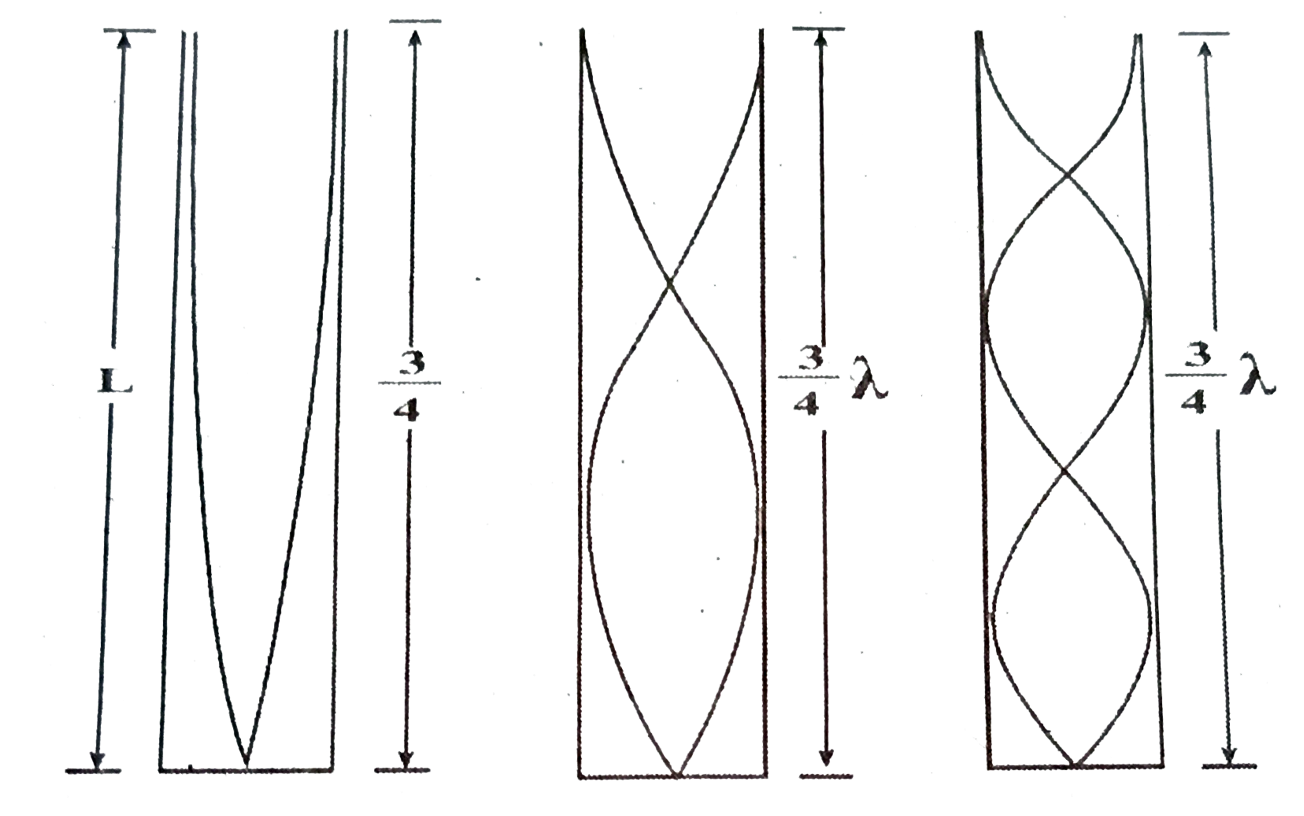
(iii) The surface of the water will act as a closed end and another as the open end. Hence, it behaves like a closed organ pipe, forming nodes at the surface of water and antinodes at the closed. end.
(iv) when a vibrating tuning fork is brought near the oepn end of tube, longitudinal waves are formed inside the air column.
(v) These waves move downward as shown in Figure, and reach the surfae of water and get reflected and produce standing waves.
(vi) The length of the air column is varied by changing the water level until a loud sound is produced in the air column.
(vii) At this particular length of frequency of waves in the air colum resonates with the frequency of the tuning fork (natural frequency of the tuning fork).
(viii) At resonance, the frequency of sound waves produced is equal to the frequency of the tuning fork. This will occure only when the length of air column is proportional to ${(\frac{1}{4})}^{t h}$ of the wavelength of the sound waves produced.
Determination of velocity of sound :
Let the first resonance occure at length $L_{1}$ , then
$\frac{1}{4} λ = L_{1} ... (1)$
But since the antinodes are note exactly formed at the open end, a correction is to included. It is called end correction e, by assuming that the antinodes is formed at some small distance above the open end. Including this end correction, the first resonane is
$\frac{1}{4} λ = L_{1} + e ... . (2)$
Now the length of the air column is increased to get the second resonance. Let $L_{2}$ be the length at which the second resonance occurs. Again tkaing end correction into account, we have
$\frac{3}{4} λ = L_{2} + e ... (3)$
In order two avoid end correction, let us take difference of equation (3) and equation (2), we get
$\frac{3}{4} λ - \frac{1}{4} λ = (L_{2} + e) - (L_{1} + e)$
$\Rightarrow \frac{1}{2} λ = L_{2} - L_{1} = Δ L$
$\Rightarrow λ = 2 Δ L$
The speed of the sound in air at room temperature can be calculated by using the formula
$v = f λ = 2 f Δ L$ .

Updated on:21/07/2023

A standing tuning fork of frequency $f$ is used to find the velocity of sound in air by resonance column appartus. The difference two resonating lengths is $1.0 m$ . Then the velocity of sound in air is
A $f m / s$
B $2 f m / s$
C $f / 2 m / s$
D $3 f m / s$
In the experiment to determine the speed of sound using a resonance column -
Aprongs of the tuning fork are kept in a vertical plane
Bprongs of the tuning fork are kept in a horizontal plane
CIn one of the two resonance observed, the length of the resonating air column is close to the wavelength of sound in air
DIn one of the two resonance obsvered, the length of the resonating air column is close to half of the wavelength of sound in air.
In the experiment to determine the speed of sound using a resonance column,
A(a) prongs of the tuning fork are kept in a vertical plane
B(b) prongs of the tuning fork are kept in a horizontal plane
C( c ) in one of the two resonance observed, the length of the resonating air column is close to the wavelength of sound in air
D( d) in one of the two resonance observed, the length of the resonating air column is close to half of the wavelength of sound in air