ABC is an isosceles triangle right-angled at C. Prove that AB2=2AC2.
Video Solution
Text Solution
In ΔABC,∠ACB=90° and AC=BC [Since, ABC is an isosceles triangle right angled at C]
Using Pythagoras theorem,
⇒(AB)2=(AC)2+(BC)2
⇒(AB)2=(AC)2+(AC)2 [Since AC = BC]
Therefore, (AB)2=2(AC)2
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
A statements of Assertion (A) is followed by a statement of Reason (R ). Mark the correct choice as.
Assertion (A): ABC is an isoseles triangle right triangle , right angled at C. Then AB2=3AC2.
Reason (R ): In an isosceles triangle ABC if AC = BC and AB2=2AC2 then ∠C=90∘.ABoth A and R are true R is the correct explanation for A.BBoth A and R are true nad R is not correct explanation for A.CA is true but R is false.DA is false but R is true.
ABC is an isosceles right triangle, right-angled at C . Prove that: AB2=2AC2.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionABC is an isosceles right-triangle right angled at C such that AC=5 cm. Then, AB= 2.5 cm (b) 5√2 cm 10 cm (d) 5 cm
View SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
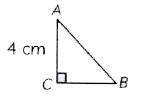 View Solution
View SolutionIn figure ABC is an isosceles triangle , right angled at C . Therefore
 View Solution
View SolutionABC is a right isosceles triangle, right angled at B.
Then sin2A+cos2C= _________View SolutionABC is an isosceles triangle with AC = BC. If AB2=2AC2, prove that ABC is a right triangle.
View Solution

