A cyclist on the ground goes round a ciruclar path of circumference 34.3 m in √22 second. The angle made by him, with the vertical, will be:-
45∘
40∘
42∘
48∘
The correct Answer is:A
To solve the problem, we need to find the angle made by the cyclist with the vertical while moving in a circular path. We will follow these steps:
Step 1: Calculate the Radius of the Circular Path
Given the circumference C=34.3m, we can use the formula for the circumference of a circle:
C=2πr
Rearranging for r:
r=C2π=34.32π
Calculating the value:
r≈34.36.2832≈5.46m
Step 2: Calculate the Velocity of the Cyclist
The time taken to complete the circular path is given as t=√22s. The velocity v can be calculated using the formula:
v=distancetime=Ct=34.3√22
Calculating the value:
v≈34.34.690≈7.31m/s
Step 3: Use the Formula to Find the Angle
We can use the relationship between the angle θ and the other parameters. The formula is:
tanθ=v2rg
Where g≈9.8m/s2 (acceleration due to gravity). Substituting the values we have:
tanθ=(7.31)2(5.46)(9.8)
Calculating v2:
v2≈53.44
Now substituting into the equation:
tanθ=53.44(5.46)(9.8)≈53.4453.468≈1
Step 4: Calculate the Angle
To find θ:
θ=tan−1(1)
This gives:
θ=45∘
Final Answer
The angle made by the cyclist with the vertical is 45∘.
---
Given the circumference C=34.3m, we can use the formula for the circumference of a circle:
The time taken to complete the circular path is given as t=√22s. The velocity v can be calculated using the formula:
We can use the relationship between the angle θ and the other parameters. The formula is:
To find θ:
The angle made by the cyclist with the vertical is 45∘.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-II
112 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - SWOE
44 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
A cyclist goes round a circular track of 440 metres length in 20 seconds Find the angle that his cycle makes with the verticle.
View SolutionA plumb bob is suspended by a light rod inside a car moving in a circular horizontal track of radius 6√35 m . The angle made by the rod with the vertical is found out to be60∘. Then, the car moves with a constant speed of ___ m/s.(g=10m/s2)
View Solution
Knowledge Check
A cyslist goes round a circular path of length 4000 m in 20 second. Calculate the angle through which he bends from vertical in order to maintain the balance
Asin−1(0.64)Btan−1(0.64)Ccos−1(0.64)DNone of theseA cyclist moves around a circular path of radius 40√3m with a speed of 20m/s. He must lean inwards at an angle θ with the vertical such that tanθ is equal to
A1B√3C1/√3D2In the previous problem. If the bullet is moving with velocity 50√2m/s, the maximum angle made by string with vertical is
A60∘B45∘Csin−1(45)Dcos−1(45)
Find the angle through which a cyclist bends when he covers a circular path 34.3m long in √22 sec . Given g=9.8ms−2 .
View SolutionA cyclist riding at a speed of 14√3ms−1 takes a turn around a circular road of radius 20√3m. What is the inclination to the vertical?
View SolutionA motor cyclist going round on unbanked circular race course has to lean inwards, making an angle 21∘49' with the vertical , in order to keep his balance. If the curve is 1 km long , then the speed of the cyclist will be,
(tan21∘49=0.4003'g=9.8m/s2)
View SolutionA man starts running with constant speed along a circular path of radius √2m He completes two rounds in 16 seconds. The magnitude of the average velocity in first 2 seconds is
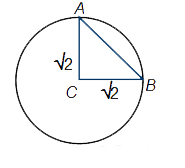
View SolutionA car is moving with constant speed of 10m/s on a horizontal circular path of radius 10√3m . A bob of mass m suspended through a light string from the roof of the car. What is the angle made by the string with the vertical if the bob is stationary with respect to the car? (g = 10 m/s2)
View Solution
