Logarithms of readings of pressure and volume for an ideal gas were plotted on a graph as shown in Fig. By measuring the gradient, it can be shwon that the gas may be
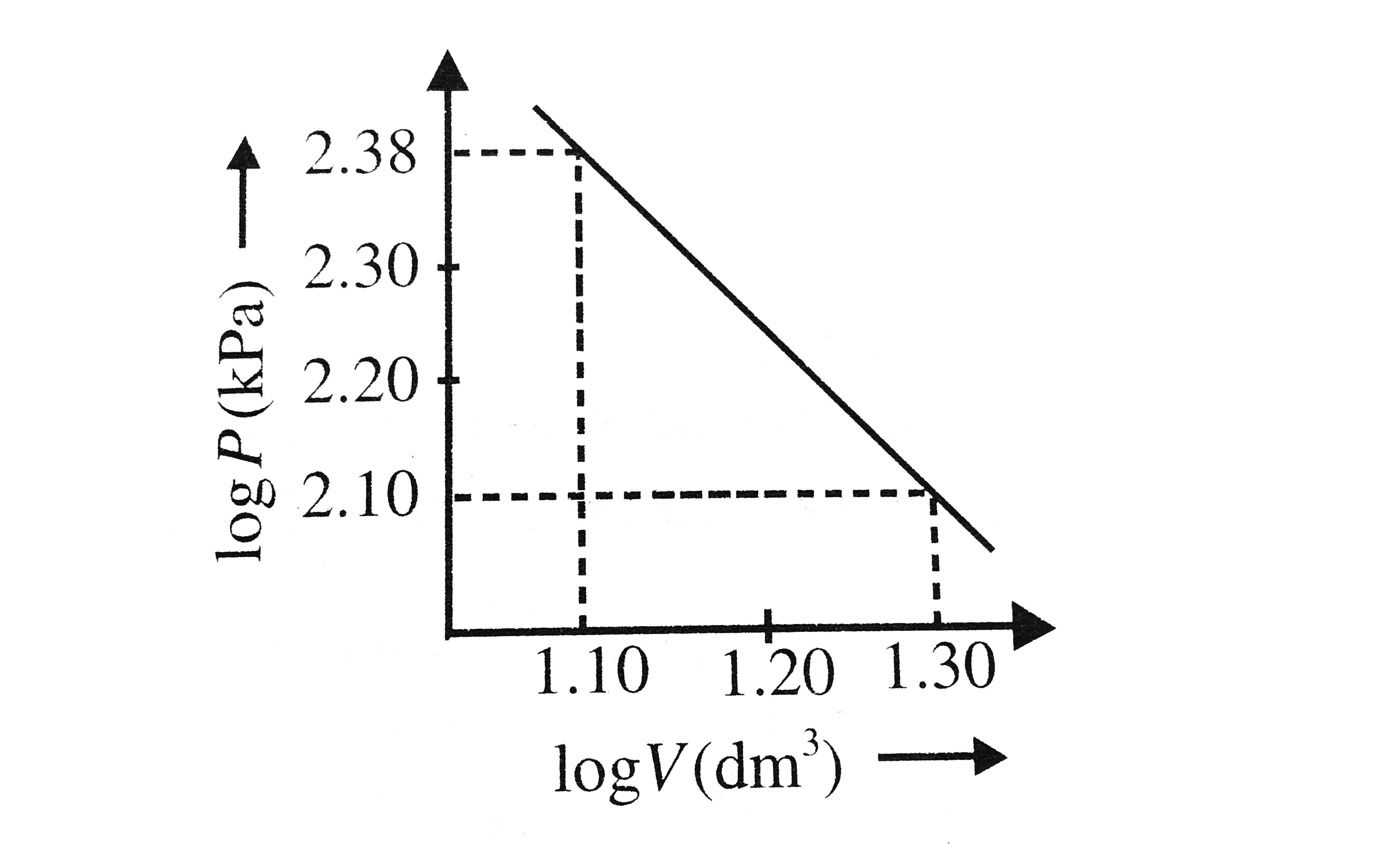
Monoatomic and undergoing an adiabatic change.
Monoatomic and undergoing an isothermal change.
Diatomic and undergoing an adiabatic change.
Triatomic and undergoing an isothermal change.
The correct Answer is:C
PVγ=C,lnP+γlnV=lnC
⇒lnP=−γlnV+lnC⇒y=mx+c
⇒m=−γ=−−[2.10−2.38](1.30−1.10)=−1.4
∴ The gas is diatomic
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
11 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
40 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Knowledge Check
The product of pressure and volume of an ideal gas is
Aa constant independent of temperatureBdirectly prouortional to square of its temperatureCdirectly proportional to its temperatureDinversely proportional to its temperatureThe product of the pressure and volume of an ideal gas is
Aa constantBapproximately equal to the universal gas constantCdirectly proportional to its temperatureDinversely proportional to its temperatureThe product of the pressure and volume of an ideal gas is
Aa constantBapproximately equal to the universal gas constantCdirectly proportional to its tempDinversely proportional to its temp
The pressure P and volume V of an ideal gas both decreases in a process.
View SolutionThe pressure p and volume V of an ideal gas both increase in a process.
View SolutionThe figure shows the graph of logarithmic reading of pressure and volume for two ideal gases A and B undergoing adiabatic process. From figure, it can be concluded that

View SolutionThe figure shows the graph of logarithmic reading of pressure and volume for two ideal gases A and B undergoing adiabatic process. From figure, it can be concluded that

View SolutionIf both the temperature and the volume of an ideal gas are doubled, the pressure
View Solution