A right angle prism(45∘−90∘−45∘) of refractive index n has a plane of refractive index n1(n1<n) cemented to its diagonal face. The assembly is in air. The ray is incident on AB.
_E01_161_Q01.png)
(i) Calculate the angle of incidence at AB for which the ray strikes the diagonal face at the critical angle .
(ii) Assuming n = 1.352 , calculate the angle of incidence at AB for which the refracted ray passes through the diagonal face undeviated.
The correct Answer is:(i)e=sin−1(1)√2[(√n2−n21)−n1] (ii) sin−1(0.956)
(i) Given that r2=C⇒r1=45∘−C & sin e = n sin(45∘−C)
sin e = n(sin45∘cos45∘sinC)
⇒e=sin−1(1)√2(√n2−n21−n1)
(ii) to pass refracted ray undeviated r2=0⇒r1=45∘ and sin e = n sin 45∘
⇒e=sin−1(1.352√2)=sin−1(0.956)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (A)35videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (B)35videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[A]23videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions427videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
A right angles prism (45∘,90∘,45∘) of refractive index n has a plate of refractive index (n1<n) cemented to its diagonal face. The assembley is in air. A ray is incident on AB.
a. Calculate the angle of incidence at AB for which the ray strikes the diagonal face at the critical angle.
b. Assuming n=1.351, calculate the angle of incidence at AB for which the refracted rey passes through the diagonal face undeviated.
View SolutionThe refracting angle of a glass prism is 60∘ and μ of its material is 1.45. Calculate angle of incidence at the first that will just reflect internaly the ray at the second face.
View Solution
Knowledge Check
- Question 1 - Select One
A ray of light passes from glass having a refractive index of 1.6, to air. The angle of incidence for which the angle of refraction is twice the angle of incidence is
Asin−1(45)Bsin−1(35)Csin−1(58)Dsin−1(25) - Question 2 - Select One
A ray of light travelling in air is incident at 45∘ on a medium of refractive index √2. The angle of refractive in the medium is
AA. 45∘BB.60∘CC.30∘DD.70∘ - Question 3 - Select One
A ray of light goes from a medium of refractive index n1 to a medium of refractive index n2. The angle of incidence is I and the angle of refraction is r. Then, sin i/sin r is equal to
An1Bn2C(n1)/(n2)D(n2)/(n1)
A prism (n=2) of apex angle 90∘ is palced in air (n=1). What should be the angle of incidence so that light ray strikes the second surface at an angle of incidence 60∘.
View SolutionA rectangular glass slab ABCD of refractive index n1 is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shwon. The maximum value of the angle of incidence αmax such that the ray comes out from the other surface CD is given by
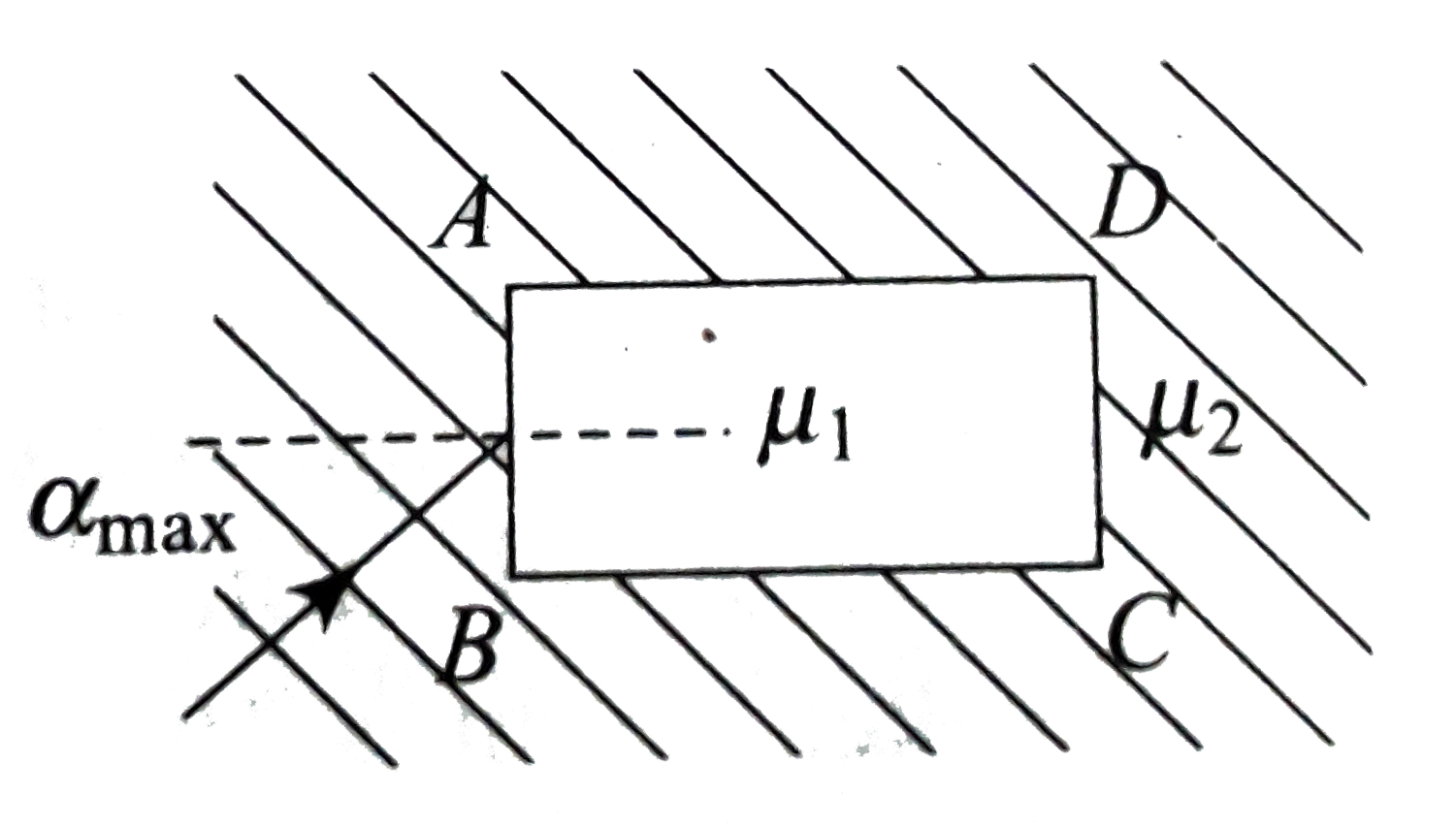View SolutionA rectengular glass slab ABCD of refractive index n_1 is immersed in water of refractive index n2(n1>n2). A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence αmax such that the ray comes out only from the other surface CD is given by
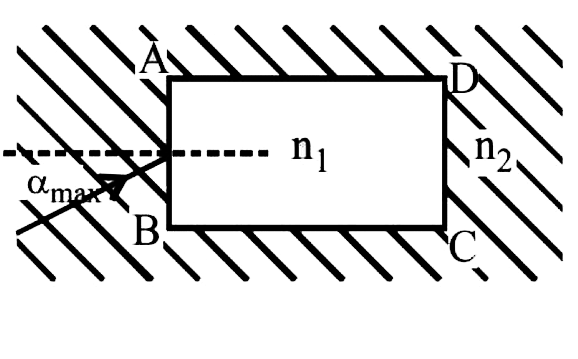View SolutionA ray of light is incident on the surface of plate of glass of refractive index 1.5 at the polarising angle. The angle of refraction of the ray will be
View SolutionA ray of light passes from vaccume into a medium of refractive index n. if the angle of incidence is twice the angle of refraction, then the angle of incidence is
View Solution