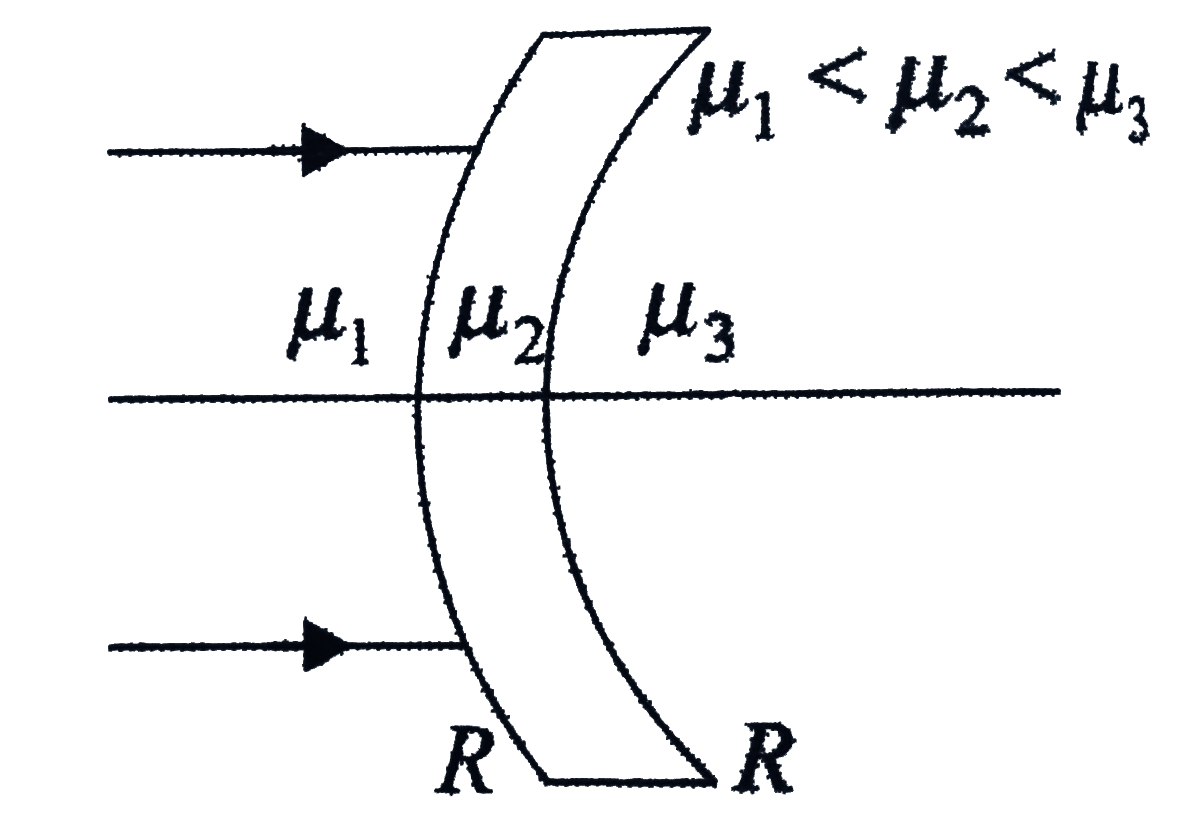
In the figure, light is incident on a thin lens as shown. The radius of curvature for both the surfaces is R. Determine the focal length of this system. 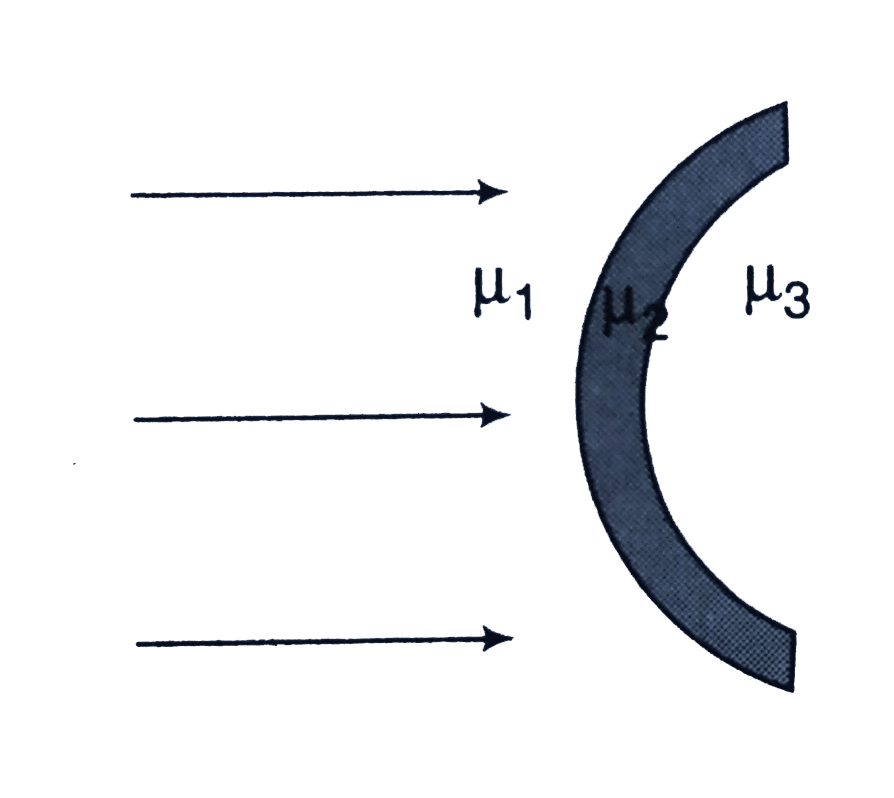
Video Solution
Text Solution
The correct Answer is:μ3Rμ3−μ1
For refraction at first surface
μ2v1−μ1−∞=μ2−μ1+R….(i)
For refraction at second surface ,
μ3v2−μ2v1=μ3−μ2+R…..(ii)
Adding equation (i) and (ii) , we get
μ3v2=μ3−μ1Rorv2=μ3Rμ3−μ1
_E01_249_S01.png)
Therefore , focal lenght of the given lens system is
μ3Rμ3−μ1
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Radius of curvature of a equi convex lens is R. Find focal length (n=32)
AR2B−R2CRD-R - Question 2 - Select One
Radius of curvature of a equi convex lens is R. Find focal length (n=32)
AR2B−R2CRD-R - Question 3 - Select One
A plano-convex lens is made of refractive index 1.6. The radius of curvature of the curved surface is 60 cm. The focal length of the lens is
A200 cmB100 cmC50 cmD400 cm
Find the focal length of the lens shown in the figure. The radii of curvature of both the surfaces are equal to R
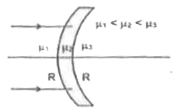 View Solution
View SolutionWhat is the refractive index of material of a plano-convex lens , if the radius of curvature of the convex surface is 10 cm and focal length of the lens is 30 cm ?
View SolutionA planoconvex lens is made of refractive index 1.6. The radius of curvature of curved surface is 60 cm. The focal length of the lens is
View SolutionA plano-convex lens is made of glass of refractive index 1.5. the radius of curvature of its convex surface is R. its focal length is
View SolutionA plano-convex lens is made of glass of refractive index 1.5. The radius of curvature of its convex surface is R. Its focal length is
View Solution